Question

10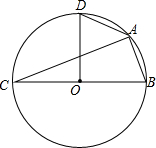．△ABC内接于⊙O，AB=2，AC=6，BC=2$\sqrt{10}$，过圆心O作OD⊥BC交⊙O于点D，连接AD，则AD的长为2$\sqrt{2}$．

Answer 1

分析 由勾股定理的逆定理得出∠BAC=90°，证出BC为⊙O的直径，得出OD=OB=$\frac{1}{2}$BC=$\sqrt{10}$，作OM⊥BC于M，ON⊥OD于N，则四边形OMAN是矩形，得出AN=OM，ON=AM，由射影定理得出AB²=BM•BC，求出BM=$\frac{\sqrt{10}}{5}$，得出AN=OM=OB-BM=$\frac{4\sqrt{10}}{5}$，由勾股定理求出AM=$\frac{3\sqrt{10}}{5}$，得出ON=AM=$\frac{3\sqrt{10}}{5}$，DN=OD-ON=$\frac{2\sqrt{10}}{5}$，再由勾股定理求出AD即可．

解答 解：∵AB=2，AC=6，BC=2$\sqrt{10}$，
∴AB²+AC²=BC²，
∴∠BAC=90°，
∴BC为⊙O的直径，
∴OD=OB=$\frac{1}{2}$BC=$\sqrt{10}$，
作OM⊥BC于M，ON⊥OD于N，如图所示：
∵OD⊥BC，
∴四边形OMAN是矩形，
∴AN=OM，ON=AM，
∵∠BAC=90°，AM⊥BC，
∴由射影定理得：AB²=BM•BC，
即2²=2$\sqrt{10}$×BM，
解得：BM=$\frac{\sqrt{10}}{5}$，
∴AN=OM=OB-BM=$\sqrt{10}$-$\frac{\sqrt{10}}{5}$=$\frac{4\sqrt{10}}{5}$，
∴AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=$\frac{3\sqrt{10}}{5}$，
∴ON=AM=$\frac{3\sqrt{10}}{5}$，
∴DN=OD-ON=$\frac{2\sqrt{10}}{5}$，
∴AD=$\sqrt{A{N}^{2}+D{N}^{2}}$=$\sqrt{8}$=2$\sqrt{2}$；
故答案为：2$\sqrt{2}$．

点评 本题考查了三角形的外接圆与圆心、勾股定理以及勾股定理的逆定理、圆周角定理、矩形的判定与性质、射影定理等知识；本题这一切，有一定难度，证明BC是直径是解决问题的关键．