题目内容

20．抛物线y=x2-4x-m的最小值为1，那么m的值为（　　）
A．-10B．-5C．10D．5

分析 直接利用配方法求出二次函数最值，进而得出关于m的等式求出即可．

解答 解：∵y=x2-4x-m
=（x-2）2-4-m，
且抛物线y=x2-4x-m的最小值为1，
∴-4-m=1，
解得：m=-5．
故选：B．

点评 此题主要考查了二次函数的最值，正确表示出二次函数最值是解题关键．

练习册系列答案
相关题目
10．已知a，b，c为正整数，且a2+b2+c2-ab-bc-ac=19，那么a+b+c的最小值等于（　　）
A．11B．10C．8D．6
11．在△ABC中，AB=6，AC=8，BC边上的中线AD是奇数，则AD=3或5．
8．设x1，x2是一元二次方程x2+5x-1=0的两个根，那么x13-11x1-3x22-16=-99．
15．函数y=$\frac{2x+8}{x+1}$的图象可由反比例函数y=$\frac{k}{x}$的图象平移得到，求k的值．
5．如图所示，有一个直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上且与AE重合，你能求出CD的长吗？
12．如图，Rt△ABC中，AC=BC=8，∠ACB=90°，F为直角边BC上一点，将纸片沿F点折叠后点B恰与BC中点D重合，得到折痕EF（E在AB边上），连接DE，再展开还原后沿DE剪开得到四边形ACDE，然后把四边形ACDE从E点开始沿射线EB平移，当A点与B点重合时停止．设平移时间为t秒（t＞0），移动速度为每秒1个单位长度，平移过程中四边形A1C1D1E1与△DEB重叠的面积为S．

（1）求DE的长；
（2）直接写出S与t的函数关系式及自变量t的取值范围；
（3）若四边形ACDE平移时，另有一动点P与四边形ACDE同时出发，以每秒$\sqrt{2}$个单位长度从点B出发沿折线BC-CA运动，求出当t为何值时，△PE1E为等腰三角形？
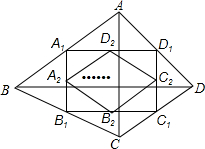9．如图，四边形ABCD中，AC=a，BD=b，且AC⊥BD，顺次连接四边形ABCD各边中点，得到四边形A1B1C1D1，再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2，…，如此进行下去，得到四边形AnBnCnDn．下列结论正确的有（　　）
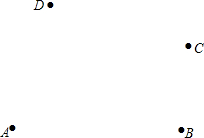①四边形A2B2C2D2是矩形；②四边形A4B4C4D4是菱形；③四边形A5B5C5D5的周长是$\frac{a+b}{4}$，④四边形AnBnCnDn的面积是$\frac{ab}{{2}^{n+1}}$．
A．1个B．2个C．3个D．4个
10．如图，平面上有A、B、C、D四点
（1）画线段AB、DC，并延长AB、DC相交于E；
（2）画直线AC、射线CB；
（3）画射线BD交AC于点F；
（4）画∠ABD的平分线BG．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网