Question

10．依次连接四边形ABCD各边的中点所得四边形是矩形，则四边形ABCD一定是（　　）

• A． 菱形
• B． 对角线相等的四边形
• C． 矩形
• D． 对角线互相垂直的四边形

Answer 1

分析 作出图形，根据三角形的中位线平行于第三边并且等于第三边的一半可得EH∥BD，EF∥AC，再根据矩形的每一个角都是直角可得∠1=90°，然后根据平行线的性质求出∠3=90°，再根据垂直定义解答即可．

解答 解：如图，连接AC、BD，
∵E、F、G、H分别是AB、BC、CD、DA的中点，
∴EH∥BD，EF∥AC，
∴∠1=∠2，∠2=∠3，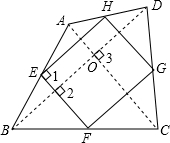
∴∠1=∠3，
∵四边形EFGH是矩形，
∴∠1=90°，
∴∠3=90°，
∴AC⊥BD，
即原四边形ABCD的对角线互相垂直，
故选D．

点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半，平行线的性质，矩形的每一个角都是直角的性质以及垂线的判定．