题目内容
8.已知分式$\frac{x+y}{2x-y}$,根据给出的条件,求解下列问题:(1)当x=1时,分式的值为0,求2x+y的值;
(2)如果|x-y|+$\sqrt{x+y-2}$=0,求分式的值.
分析 (1)根据分式的分子为零分母不为零,可得方程组,根据解方程组,可得x、y的值,根据代数式求值,可得答案;
(2)根据非负数的和为零,可得每个非负数同时为零,根据代数式求值,可得答案.
解答 解:(1)由x=1时,分式的值为0,得
$\left\{\begin{array}{l}{x+y=0}\\{2x-y≠0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$.
2x+y=2+(-1)=1;
(2)由如果|x-y|+$\sqrt{x+y-2}$=0,得
$\left\{\begin{array}{l}{x-y=0}\\{x+y-2=0}\end{array}\right.$
,解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
$\frac{x+y}{2x-y}$=2.
点评 本题考查了分式的值,(1)利用分式值为零的条件得出方程组是解题关键;(2)利用非负数的和为零得出每个非负数同时为零是解题关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
3.若∠α与∠β是内错角,且∠α=50°时,则∠β的度数为( )
| A. | 50° | B. | 130° | C. | 50°或130° | D. | 无法确定 |
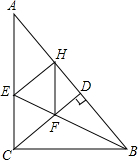 已知,如图,△ABC中,∠ACB=90°,BE平分∠ABC,CD⊥AB于D,EH⊥B于H,CD交BE于F,求证:四边形CEHF为菱形.
已知,如图,△ABC中,∠ACB=90°,BE平分∠ABC,CD⊥AB于D,EH⊥B于H,CD交BE于F,求证:四边形CEHF为菱形.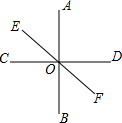 如图所示,直线AB、CD、EF相交于点O,AB⊥CD,∠AOE=$\frac{1}{2}$∠AOD,求∠BOF与∠BOE的度数.
如图所示,直线AB、CD、EF相交于点O,AB⊥CD,∠AOE=$\frac{1}{2}$∠AOD,求∠BOF与∠BOE的度数.
 如图,在△ABC中,∠BAC=90°,AC=6,BC=10,过点A的直线DE∥BC,∠ABC与∠ACB的平分线分别交DE于E、D,则DE的长为( )
如图,在△ABC中,∠BAC=90°,AC=6,BC=10,过点A的直线DE∥BC,∠ABC与∠ACB的平分线分别交DE于E、D,则DE的长为( )