题目内容
 如图,A、B、C三点在一条直线上,分别以AB、BC为边,在AC的同侧作等边△ABD和△BCE,连接AE、CD.求证:AE=DC.
如图,A、B、C三点在一条直线上,分别以AB、BC为边,在AC的同侧作等边△ABD和△BCE,连接AE、CD.求证:AE=DC.考点:全等三角形的判定与性质,等边三角形的性质
专题:证明题
分析:先由△ABD和△BCE是等边三角形,可知AB=DB,BE=CB,∠DBA=60°,∠EBC=60°,故可得出∠ABE=∠DBC,根据SAS定理可知△ABE≌△DBC,由全等三角形的性质即可得出结论.
解答:证明:∵△ABD和△BCE是等边三角形,
∴AB=DB,CB=BE,∠ABD=∠CBE=60°,
∵∠DCA=∠ECB=60°,
∴∠ABD+∠DBE=∠CBE+∠DBE,
∴∠ABE=∠CBD.
在△ABE与△DBC中,
∵
,
∴△ABE≌△DBC,
∴AE=DC.
∴AB=DB,CB=BE,∠ABD=∠CBE=60°,
∵∠DCA=∠ECB=60°,
∴∠ABD+∠DBE=∠CBE+∠DBE,
∴∠ABE=∠CBD.
在△ABE与△DBC中,
∵
|
∴△ABE≌△DBC,
∴AE=DC.
点评:题考查的是等边三角形的判定与性质及全等三角形的判定与性质,根据题意判断出△ABE≌△DBC是解答此题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
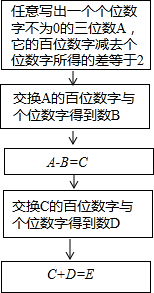 阅读右边的框图并回答下列问题:
阅读右边的框图并回答下列问题: