题目内容
7. 在平面直角坐标系xOy中,直线y=-x+2与y轴交于点A,点A关于x轴的对称点为B,过点B作y轴的垂线l,直线l与直线y=-x+2交于点C;抛物线y=nx2-2nx+n+2(其中n<0)的顶点坐标为D.
在平面直角坐标系xOy中,直线y=-x+2与y轴交于点A,点A关于x轴的对称点为B,过点B作y轴的垂线l,直线l与直线y=-x+2交于点C;抛物线y=nx2-2nx+n+2(其中n<0)的顶点坐标为D.(1)求点C,D的坐标;
(2)若点E(2,-2)在抛物线y=nx2-2nx+n+2(其中n<0)上,求n的值;
(3)若抛物线y=nx2-2nx+n+2(其中n<0)与线段BC有唯一公共点,求n的取值范围.
分析 (1)根据题意分别求出点A、B、C的坐标,再讲二次函数配方可得顶点D的坐标;
(2)将点E坐标代入,解方程即可得;
(3)根据题意知当x=0时y>-2,当x=4时y≤-2,列不等式组求解可得.
解答 解:(1)y=-x+2中当x=0时,y=2,
∴点A(0,2),
∵点A关于x轴的对称点为B,
∴点B(0,-2),
∵点B垂直于y轴的直线l与直线y=-x+2交于点C,
∴当y=-2时,-x+2=-2,
解得:x=4,
即点C(4,-2);
∵y=nx2-2nx+n+2=n(x-1)2+2,
∴顶点D的坐标为(1,2);
(2)将点E(2,-2)代入y=nx2-2nx+n+2,得:-2=4n-4n+n+2,
解得:n=-4;
(3)根据题意知当x=0时y>-2,当x=4时y≤-2,
即$\left\{\begin{array}{l}{n+2>-2}\\{16n-8n+n+2≤-2}\end{array}\right.$,
解得:-4<n≤-$\frac{4}{9}$.
点评 本题主要考查二次函数的性质,根据题意得出关于n的不等式组是解题的关键.

练习册系列答案
相关题目
18.下列各式的计算,结果正确的是( )
| A. | 3a+2b=5ab | B. | m2-n2=0 | C. | 5x+2x=7x2 | D. | 5xy-5yx=0 |
2.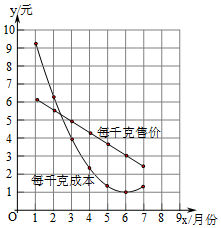 在1~7月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是( )
在1~7月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是( )
 在1~7月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是( )
在1~7月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是( )| A. | 1月份 | B. | 2月份 | C. | 5月份 | D. | 7月份 |
19.下列运算中正确的是( )
| A. | x2÷x8=x-4 | B. | a•a2=a2 | C. | (a3)2=a6 | D. | (3a)3=9a3 |
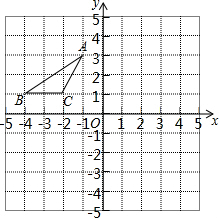 如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)(-2,1),先将△ABC向右平移5个单位,向上平移1个单位得△A1B1C1,再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2,点A1的对应点为点A2.
如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)(-2,1),先将△ABC向右平移5个单位,向上平移1个单位得△A1B1C1,再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2,点A1的对应点为点A2.