Question

5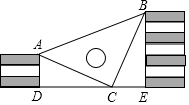．王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AC=BC，∠ACB=90°），点C在DE上，点A和B分别与木墙的顶端重合，求两堵木墙之间的距离．

Answer 1

分析 根据题意可得AC=BC，∠ACB=90°，AD⊥DE，BE⊥DE，进而得到∠ADC=∠CEB=90°，再根据等角的余角相等可得∠BCE=∠DAC，再证明△ADC≌△CEB即可，利用全等三角形的性质进行解答．

解答 解：由题意得：AC=BC，∠ACB=90°，AD⊥DE，BE⊥DE，
∴∠ADC=∠CEB=90°，
∴∠ACD+∠BCE=90°，∠ACD+∠DAC=90°，
∴∠BCE=∠DAC，
在△ADC和△CEB中，
$\left\{\begin{array}{l}{∠ADC=∠CEB}\\{∠DAC=∠BCE}\\{AC=BC}\end{array}\right.$，
∴△ADC≌△CEB（AAS）；
由题意得：AD=EC=6cm，DC=BE=14cm，
∴DE=DC+CE=20（cm），
答：两堵木墙之间的距离为20cm．

点评 此题主要考查了全等三角形的应用，关键是正确找出证明三角形全等的条件．