题目内容
20．
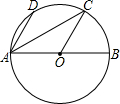如图，AB是⊙O的直径，点D，C在⊙O上，AD∥OC，∠DAB=60°，连接AC，则∠DAC等于（ ）| A． | 20° | B． | 30° | C． | 25° | D． | 40° |
分析 首先利用同一圆的半径相等和平行线的性质得到∠DAC=∠CAB，然后利用已知角求解即可．
解答 解：∵OA=OC，
∴∠CAO=∠ACO，
∵AD∥OC，
∴∠DAC=∠ACO，
∴∠DAC=∠CAB，
∵∠DAB=60°，
∴∠DAC=$\frac{1}{2}$∠DAB=30°．
故选B．
点评 本题考查的是圆周角定理，熟知平行线的性质及同一圆的半径是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
10．
如图，将含30°角的三角板的直角顶点放在直尺的一边上，若∠1=40°，则∠2的度数为（ ）
如图，将含30°角的三角板的直角顶点放在直尺的一边上，若∠1=40°，则∠2的度数为（ ）| A． | 90° | B． | 80° | C． | 75° | D． | 70° |
11．温度上升-3摄氏度后，又下降3摄氏度，实际是（ ）
| A． | 上升1℃ | B． | 上升6℃ | C． | 下降6℃ | D． | 不变 |
8．两个地区当地时间之间的差别称为时差，小华的爸爸经常去国外出差，为了方便了解爸爸所出差城市的时间，小华记录了几个外国城市与北京的时差（单位：小时）（以北京时间为标准时间，比标准时间晚的用正数表示，比标准时间早的用负数表示），如表：
（1）6月20日，小华吃早饭的时间是北京时间早上7：30，求此时伦敦、奥克兰和悉尼的时间；
（2）小华的爸爸于北京时间7月16日上午9：00从北京首都机场坐CA989航班飞往纽约，该航班需航行13个小时才能到达纽约，求小华的爸爸到达纽约时，纽约的当地时间；
（3）小华于北京时间7月19日下午2点想给在纽约的爸爸打电话，你认为合适吗？
| 城市 | 伦敦 | 奥克兰 | 纽约 | 悉尼 |
| 时差 | -7 | +4 | -12 | +2 |
（2）小华的爸爸于北京时间7月16日上午9：00从北京首都机场坐CA989航班飞往纽约，该航班需航行13个小时才能到达纽约，求小华的爸爸到达纽约时，纽约的当地时间；
（3）小华于北京时间7月19日下午2点想给在纽约的爸爸打电话，你认为合适吗？
15．下面四组图形中，必是相似三角形的为（ ）
| A． | 有一个角为40°的两个等腰三角形 | |
| B． | 两个直角三角形 | |
| C． | 两条边对应成比例，一个对应角相等的两个三角形 | |
| D． | 有一个角为100°的两个等腰三角形 |