题目内容
11.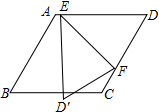 如图,在菱形ABCD中,对角线长AC=2,BD=2$\sqrt{3}$,点E、F在边AD、CD上,以直线EF为折痕折叠,若ED⊥ED′,则∠D′FC的度数为30°.
如图,在菱形ABCD中,对角线长AC=2,BD=2$\sqrt{3}$,点E、F在边AD、CD上,以直线EF为折痕折叠,若ED⊥ED′,则∠D′FC的度数为30°.
分析 首先连接AC,BD,相较于点O,由在菱形ABCD中,对角线长AC=2,BD=2$\sqrt{3}$,可求得∠ADC=60°,又由以直线EF为折痕折叠,若ED⊥ED′,即可求得∠DEF的度数,继而求得答案.
解答  解:连接AC,BD,相较于点O,
解:连接AC,BD,相较于点O,
∵在菱形ABCD中,对角线长AC=2,BD=2$\sqrt{3}$,
∴OA=1,0D=$\sqrt{3}$,AC⊥BD,
∴tan∠ADO=$\frac{OA}{OD}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠ADO=30°,
∴∠ADC=2∠ADO=60°,
∵ED⊥ED′,
∴∠DEF=$\frac{1}{2}$∠DED′=45°,
∴∠DFE=180°-∠DEF-∠ADC=75°,
∴∠D′FE=′DFE=75°,
∴∠D′FC=180°-∠DFE-∠D′FE=30°.
故答案为:30°.
点评 此题考查了菱形的性质、折叠的性质以及三角函数等知识.注意准确作出辅助线是解此题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
2.下列方程中,是二元一次方程的是( )
| A. | xy=2 | B. | 2x=y | C. | 2x=2 | D. | x2=y |
16.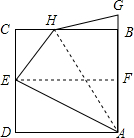 将正方形纸片ABCD按如图所示对折,使边AD与BC重合,折痕为EF,连接AE,将AE折叠到AB上,折痕为AH,则$\frac{BH}{BC}$的值是$\frac{\sqrt{5}-1}{2}$.
将正方形纸片ABCD按如图所示对折,使边AD与BC重合,折痕为EF,连接AE,将AE折叠到AB上,折痕为AH,则$\frac{BH}{BC}$的值是$\frac{\sqrt{5}-1}{2}$.
 将正方形纸片ABCD按如图所示对折,使边AD与BC重合,折痕为EF,连接AE,将AE折叠到AB上,折痕为AH,则$\frac{BH}{BC}$的值是$\frac{\sqrt{5}-1}{2}$.
将正方形纸片ABCD按如图所示对折,使边AD与BC重合,折痕为EF,连接AE,将AE折叠到AB上,折痕为AH,则$\frac{BH}{BC}$的值是$\frac{\sqrt{5}-1}{2}$.
20.一组数据2,3,5,4,4,6的中位数和平均数分别是( )
| A. | 4.5和4 | B. | 4和4 | C. | 4和4.8 | D. | 5和4 |
1.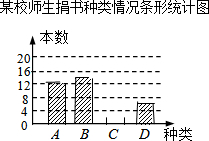 在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:
在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:
某校师生捐书种类情况统计表
(1)统计表中的m=8,n=30%;
(2)补全条形统计图;
(3)本次活动师生共捐书2000本,请估计有多少本科普类图书?
 在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:
在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:某校师生捐书种类情况统计表
| 种类 | 频数 | 百分比 |
| A.科普类 | 12 | n |
| B.文学类 | 14 | 35% |
| C.艺术类 | m | 20% |
| D.其它类 | 6 | 15% |
(2)补全条形统计图;
(3)本次活动师生共捐书2000本,请估计有多少本科普类图书?