��Ŀ����
5�� ��ͼ����ƽ��ֱ������ϵxOy�У����κ���y=ax2+bx�Ķ���ΪD��1��-1��������x�ύ��O��A���㣬���κ���y=ax2+bx��ͼ�����G1����G1����ƽ��m��m��0������λ�õ���ͼ�����G2��G2��x�ύ��B��C���㣬��G2��G1�ཻ�ڵ�P��
��ͼ����ƽ��ֱ������ϵxOy�У����κ���y=ax2+bx�Ķ���ΪD��1��-1��������x�ύ��O��A���㣬���κ���y=ax2+bx��ͼ�����G1����G1����ƽ��m��m��0������λ�õ���ͼ�����G2��G2��x�ύ��B��C���㣬��G2��G1�ཻ�ڵ�P����1������a��b��ֵ��
����G2�ĺ�������ʽ���ú�m��ʽ�ӱ�ʾ����
��2������PBC���������S����S��m�Ĺ�ϵʽ��
��3���Ƿ���ڡ�PBC������ǡ�DAB�������3���������ڣ�ֱ��д��m��ֵ���������ڣ�˵�����ɣ�
���� ��1����ֱ�Ӹ��ݶ���ΪD��1��-1�����a��b��ֵ���ɣ�
���Ȱ�������G1��Ϊ����ʽ����ʽ������ͼ��ƽ�Ƶ����ʼ��ɵó����ۣ�
��2������M��ʾ��P�����꣬�ٷ�m��2��m��2��������������ۣ�
��3������m��2��m��2�ó���DAB����ı���ʽ�������ɵó����ۣ�
��� �⣺��1���١߶��κ���y=ax2+bx��a��0���Ķ���Ϊ��1��-1����
��$\left\{\begin{array}{l}-\frac{b}{2a}=1\\ a+b=-1\end{array}\right.$
��a=1��b=-2��
���ɣ�1����G1�Ľ���ʽΪy=x2-2x����y=��x-1��2-1��
��G2�ǰ�G1����ƽ��m��m��0������λ�õ��ģ�
��G2�Ľ���ʽΪy=��x-1-m��2-1��
��2����G2��G1����ƽ��m��m��0������λ�õ��ģ�A��2��0����
���P�ĺ�����Ϊ$\frac{m+2}{2}$��
��G2��G1�ཻ�ڵ�P��
���P������$\frac{m+2}{2}$��$\frac{1}{4}$m2-1����
����ͼ1��
��m��2ʱ��
��S��PBC=$\frac{1}{2}$��2����1-$\frac{1}{4}$m2����
��S=-$\frac{1}{4}$m2+1��m��2����
����ͼ2����m��2ʱ��
S��PBC=$\frac{1}{2}$��2����$\frac{1}{4}$m2-1����
��S=-$\frac{1}{4}$m2-1��m��2����
��3����m��2ʱ��
��A��2��0����B��m��0����
��AB=2-m��
��D��1��-1����
��S��DAB=$\frac{1}{2}$��1����2-m����
�ߡ�PBC������ǡ�DAB�������3����
��-$\frac{1}{4}$m2+1=$\frac{3}{2}$��2-m����������4m2-6m+8=0���˷����⣬�ʴ�����������ڣ�
��m��2ʱ��AM=m-2��
�ߡ�PBC������ǡ�DAB�������3����
��-$\frac{1}{4}$m2-1=3��$\frac{1}{2}$����m-2�������m=2����ȥ����m=4��
��m=4��
���� ���⿼����Ƕ��κ����ۺ��⣬�漰�����κ���ƽ�Ƶ����ʼ������ε������ʽ��֪ʶ���ڽ��2������3��ʱҪע����з������ۣ�

| A�� | 20�� | B�� | 15�� | C�� | 10�� | D�� | 9�� |
| A�� | һ��Ա�ƽ������ȵ��ı�����ƽ���ı��� | |
| B�� | �Խ�����ȵ�ƽ���ı����Ǿ��� | |
| C�� | һ���ڱ���ȵ�ƽ���ı��������� | |
| D�� | ��һ������ֱ�ǵ�ƽ���ı����������� |

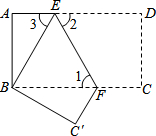 ��ͼ���ѳ�����ֽƬABCD��EF�۵���ʹ�õ�D���B�غϣ���C���ڵ�C���λ���ϣ�
��ͼ���ѳ�����ֽƬABCD��EF�۵���ʹ�õ�D���B�غϣ���C���ڵ�C���λ���ϣ�