题目内容
3. 矩形ABCD中,AB=5,BC=3,P在AD上,Q在AB上,将矩形沿PQ折叠使点A落在CD上的点A1,求点A1能够移动的最大距离.
矩形ABCD中,AB=5,BC=3,P在AD上,Q在AB上,将矩形沿PQ折叠使点A落在CD上的点A1,求点A1能够移动的最大距离.
分析 当点Q与点B重合时,A1D最短;由折叠的性质得出A1B=AB=5,由矩形的性质得出∠C=90°,CD=AB=5,AD=BC=3,由勾股定理求出A1C=4,得出A1D=1;当点P与点D重合时,A1D最长;此时A2D=AD=3;即可得出结果.
解答 解: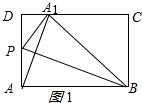 当点Q与点B重合时,A1D最短;
当点Q与点B重合时,A1D最短;
如图1所示:
由折叠的性质得:A1B=AB=5,
∵四边形ABCD是矩形,
∴∠C=90°,CD=AB=5,AD=BC=3,
∴A1C=$\sqrt{{5}^{2}-{3}^{2}}$=4,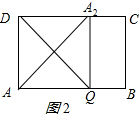
∴A1D=5-4=1;
当点P与点D重合时,A1D最长;
如图2所示:
此时A2D=AD=3;
∴点A1能够移动的最大距离=3-1=2.
点评 本题考查了矩形的性质、折叠的性质、勾股定理;熟练掌握矩形的性质和折叠的性质是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知:P($\frac{3m-2}{5}$,$\frac{m+1}{3}$)点在y轴上,则P点的坐标为( )
| A. | (0,-$\frac{5}{9}$) | B. | ($\frac{7}{9}$,0) | C. | (0,$\frac{5}{9}$) | D. | (-$\frac{5}{9}$,0) |
15.平行四边形的两条对角线分别为4和6,则其中一条边x的取值范围为( )
| A. | 2<x<3 | B. | 1<x<5 | C. | 0<x<4 | D. | 0<x<6 |
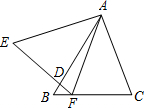 如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:
如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论: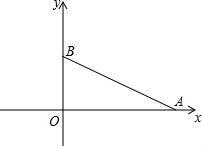 如图,在平面直角坐标系中有两点A(4,0),B(0,2),如果点C在x轴上(C与A不重合)当点C的坐标为(1,0)或(-1,0)时,使得△BOC∽△AOB.
如图,在平面直角坐标系中有两点A(4,0),B(0,2),如果点C在x轴上(C与A不重合)当点C的坐标为(1,0)或(-1,0)时,使得△BOC∽△AOB.