题目内容
18.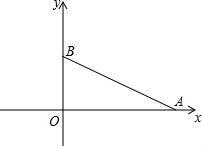 如图,在平面直角坐标系中有两点A(4,0),B(0,2),如果点C在x轴上(C与A不重合)当点C的坐标为(1,0)或(-1,0)时,使得△BOC∽△AOB.
如图,在平面直角坐标系中有两点A(4,0),B(0,2),如果点C在x轴上(C与A不重合)当点C的坐标为(1,0)或(-1,0)时,使得△BOC∽△AOB.
分析 根据△BOC∽△AOB,得出$\frac{BO}{AO}$=$\frac{OC}{OB}$,再根据A、B点的坐标,即可得出答案.
解答 解:∵△BOC∽△AOB,
∴$\frac{BO}{AO}$=$\frac{OC}{OB}$,
∴$\frac{2}{4}$=$\frac{OC}{2}$,
∴OC=1,
∵点C在x轴上,
∴点C的坐标为(1,0)或(-1,0)
故答案为:(1,0)或(-1,0).
点评 本题考查了相似三角形的判定、坐标与图形性质.解答此类题目时,首先判断由B、O、C三点组成的三角形形状,再利用两个三角形直角边与直角边对应关系的两种可能,分别求解.

练习册系列答案
相关题目
9.下列几种说法:
①两点之间线段最短;
②任何数的平方都是正数;
③几个角的和等于180°,我们就说这几个角互补;
④34x3是7次单项式;
⑤同旁内角的角平分线相互垂直.
其中正确的语句有( )句.
①两点之间线段最短;
②任何数的平方都是正数;
③几个角的和等于180°,我们就说这几个角互补;
④34x3是7次单项式;
⑤同旁内角的角平分线相互垂直.
其中正确的语句有( )句.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.一元二次方程x(2x+3)=5的常数项是( )
| A. | -5 | B. | 2 | C. | 3 | D. | 5 |
8.从标号分别为1、2、3、4、5张卡片中随机抽取1张,下列事件是不可能事件的是( )
| A. | 该卡标号小于6 | B. | 该卡标号大于6 | C. | 该卡标号是奇数 | D. | 该卡标号是3 |
 如图所示,△ABC的底边BC上的高是6cm,当三角形的顶点C沿底边所在直线向点B运动时,三角形的面积发生了变化.在这个变化过程中,变量是BC,常量是6cm.
如图所示,△ABC的底边BC上的高是6cm,当三角形的顶点C沿底边所在直线向点B运动时,三角形的面积发生了变化.在这个变化过程中,变量是BC,常量是6cm. 矩形ABCD中,AB=5,BC=3,P在AD上,Q在AB上,将矩形沿PQ折叠使点A落在CD上的点A1,求点A1能够移动的最大距离.
矩形ABCD中,AB=5,BC=3,P在AD上,Q在AB上,将矩形沿PQ折叠使点A落在CD上的点A1,求点A1能够移动的最大距离. 有两个构造完全相同(除所标数字外)的转盘A、B,游戏规定:转动两个转盘各一次,指向大的数字获胜.
有两个构造完全相同(除所标数字外)的转盘A、B,游戏规定:转动两个转盘各一次,指向大的数字获胜.