题目内容
14.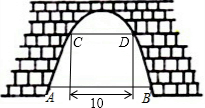 如图是一座抛物线拱形桥,在正常水位时,水面AB宽是20m,水位上升3m就达到警戒线CD,这是水面宽度为10m,请构建适当的水平直角坐标系求抛物线所对应的函数表达式,并求水位到达警戒线时拱顶与水面之间的距离.
如图是一座抛物线拱形桥,在正常水位时,水面AB宽是20m,水位上升3m就达到警戒线CD,这是水面宽度为10m,请构建适当的水平直角坐标系求抛物线所对应的函数表达式,并求水位到达警戒线时拱顶与水面之间的距离.
分析 以拱桥最顶端为原点,建立直角坐标系,根据题目中所给的数据求出函数解析式即可.
解答 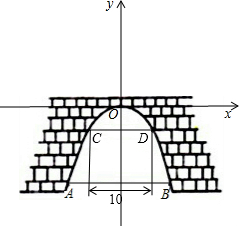 解:解立如图所示的平面直角坐标系,
解:解立如图所示的平面直角坐标系,
设抛物线解析式为y=ax2,
因为抛物线关于y轴对称,AB=20,所以点B的横坐标为10,
设点B(10,n),点D(5,n+3),
由题意:$\left\{\begin{array}{l}{n=100a}\\{n+3=25a}\end{array}\right.$,
解得$\left\{\begin{array}{l}{n=-4}\\{a=-\frac{1}{25}}\end{array}\right.$,
∴y=-$\frac{1}{25}$x2.
∴n+3=-1,
∴水位到达警戒线时拱顶与水面之间的距离为1m.
点评 此题考查了二次函数的应用,用待定系数法求二次函数的解析式,解题关键是建立适当的平面直角坐标系.

练习册系列答案
相关题目
19.下列方程中一定是一元二次方程的是( )
| A. | 5x2-$\frac{2}{x}$+2=0 | B. | ax2+bx+c=0 | C. | 2x+3=6 | D. | (a2+2)x2-2x+3=0 |
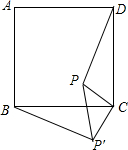 如图,P是正方形ABCD内一点,将△PCD绕点C逆时针方向旋转后与△P′CB重合,若PC=1,则PP′=$\sqrt{2}$.
如图,P是正方形ABCD内一点,将△PCD绕点C逆时针方向旋转后与△P′CB重合,若PC=1,则PP′=$\sqrt{2}$. 如图,直线a∥b,∠1=115°,求∠2的度数.
如图,直线a∥b,∠1=115°,求∠2的度数.