题目内容
在实数范围内,方程x2=-1无解,为使开方运算在负数范围内可以进行,我们规定i2=-1.定义一种新数:Z=a+bi({a、b为实数}),并规定实数范围内的所有运算法则对于新数Z=a+bi?({a、b为实数});仍然成立.例如:Z2=(a+bi)2=(a+bi)•(a+bi)=a2+2a•bi+(bi)2=a2-b2+2abi,若Z=-| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
(1)若Z=-
| 1 |
| 2 |
| ||
| 2 |
(2)若Z=-
| 1 |
| 2 |
| ||
| 2 |
分析:(1)由于Z3=z2×z,把已求得的z2的值代入即可;
(2)由于z=-
+
i,z2=-
-
i,z3=1,z4=-
+
i,可得到3个为一轮,依次循环.那么2008÷3=669…1,那么z2008应和z的值相等,由此即可求解.
(2)由于z=-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
解答:解:(1)Z3=z2×z
=(-
-
i)×(-
+
i)
=
-(
i)2
=
-
×(-1)
=1;
(2)z=-
+
i,z2=-
-
i,z3=1,z4=-
+
i,
∵2008÷3=669…1,
∴z2008应和z的值相等,z2008=-
+
i.
=(-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=
| 1 |
| 4 |
| ||
| 2 |
=
| 1 |
| 4 |
| 3 |
| 4 |
=1;
(2)z=-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∵2008÷3=669…1,
∴z2008应和z的值相等,z2008=-
| 1 |
| 2 |
| ||
| 2 |
点评:此题主要考查了实数和代数式的运算及对知识迁移运用能力,计算分析,得到相应规律是解决本题的关键.

练习册系列答案
相关题目
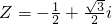 ,则
,则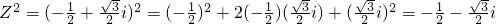 ,依据上述规定,
,依据上述规定, ,则
,则 ,依据上述规定,
,依据上述规定,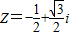 ,试求Z3的值;
,试求Z3的值; ,试求z2008的值.
,试求z2008的值.