题目内容
13.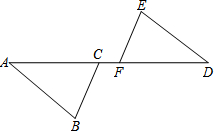 已知:如图,AB∥DE,且AB=DE,AF=DC,求证:BC=EF.
已知:如图,AB∥DE,且AB=DE,AF=DC,求证:BC=EF.
分析 根据两直线平行,内错角相等可得∠A=∠D,再求出AC=DF,然后利用“边角边”证明△ABC和△DEF全等,根据全等三角形对应边相等证明即可.
解答 证明:∵AB∥DE,
∴∠A=∠D,
∵AF=DC,
∴AF-CF=DC-CF,
即AC=DF,
在△ABC和△DEF中,$\left\{\begin{array}{l}{AB=DE}\\{∠A=∠D}\\{AC=DF}\end{array}\right.$,
∴△ABC≌△DEF(SAS),
∴BC=EF.
点评 本题考查了全等三角形的判定与性质,平行线的性质,熟练掌握三角形全等的判定方法并准确识图是解题的关键.

练习册系列答案
相关题目
5.一组数据2,6,-4,5,-2,|-4|,2,则这组数据的众数是( )
| A. | 2 | B. | 4 | C. | 6 | D. | -4 |
 如图,在△ABC中,∠BAC=80°,∠B=35°AD平分∠BAC,则∠ADC的度数为75°.
如图,在△ABC中,∠BAC=80°,∠B=35°AD平分∠BAC,则∠ADC的度数为75°.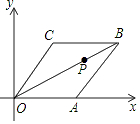 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为($\frac{10}{7}$,$\frac{5}{7}$).
已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为($\frac{10}{7}$,$\frac{5}{7}$). 在Rt△ABC中,∠ACB=90°,利用尺规在AC边上求作一点P,使PB+PC=AC,(保留作图痕迹,不写作法.)
在Rt△ABC中,∠ACB=90°,利用尺规在AC边上求作一点P,使PB+PC=AC,(保留作图痕迹,不写作法.)