题目内容
5.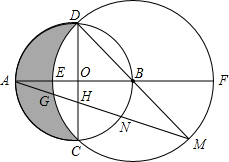 如图,已知⊙O的半径为R,直径AB⊥直径CD,以B为圆心,以BD为半径作⊙B交AB于E,交AB的延长线于F,连接DB并延长交⊙O于M,连接MA交⊙O于N,交CD于H,交⊙B于G.
如图,已知⊙O的半径为R,直径AB⊥直径CD,以B为圆心,以BD为半径作⊙B交AB于E,交AB的延长线于F,连接DB并延长交⊙O于M,连接MA交⊙O于N,交CD于H,交⊙B于G.(1)求图中阴影部分的面积S;
(2)求证:HA•HN=HG•HM.
分析 (1)连接BC,由直径AB⊥直径CD,得到∠DBC=90°,于是得到BD=$\sqrt{2}$R,求出S弓形DEC=S扇形BDC-S△BDC=$\frac{90•π•(\sqrt{2}R)^{2}}{360}$-$\frac{1}{2}$$\sqrt{2}R•\sqrt{2}R$=$\frac{π}{2}{R}^{2}$-R2,于是求得S阴影=S半圆-S弓形DEC=$\frac{1}{2}π{R}^{2}$-($\frac{π}{2}{R}^{2}$-R2)=R2;
(2)根据相交弦定理和等量代换即可得到结论.
解答 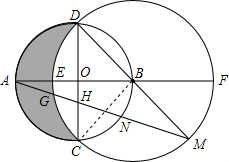 解:(1)连接BC,
解:(1)连接BC,
∵直径AB⊥直径CD,
∴∠DBC=90°,
∵OB=R,
∴BD=$\sqrt{2}$R,
∴S弓形DEC=S扇形BDC-S△BDC=$\frac{90•π•(\sqrt{2}R)^{2}}{360}$-$\frac{1}{2}$$\sqrt{2}R•\sqrt{2}R$=$\frac{π}{2}{R}^{2}$-R2,
∴S阴影=S半圆-S弓形DEC=$\frac{1}{2}π{R}^{2}$-($\frac{π}{2}{R}^{2}$-R2)=R2;
(2)在⊙O中,由相交弦定理得:AH•HN=CH•DH,
在⊙B中,由相交弦定理得:CH•DH=GH•HM,
∴AH•HN=GH•HM.
点评 本题考查了相似三角形的判定和性质,相交弦定理,扇形的面积,等腰直角三角形的面积,熟练掌握各定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列各式中正确的是( )
| A. | -(-2)>-1 | B. | |-0.2|=-0.2 | C. | |-5|<0 | D. | -$\frac{3}{2}$>-$\frac{1}{2}$ |
20.先阅读下列一段文字,然后解答问题:
某运输部门规定:办理托运,当一种物品的重量不超过16千克时,需付基础费30元和保险费a元:为限制过重物品的托运,当一件物品超过16千克时,除了付以上基础费和保险费外,超过部分每千克还需付b元超重费.设某件物品的重量为x千克.
(1)当x≤16时,支付费用为a+30元(用含a的代数式表示);当x≥16时,支付费用为a+30+(x-16)b元(用含x和a、b的代数式表示);
(2)甲、乙两人各托运一件物晶,物品重量和支付费用如下表所示
①试根据以上提供的信息确定a,b的值.
②试问在物品可拆分的情况下,用不超过105元的费用能否托运50千克物品?若能,请设计出其中一种托运方案,并求出托运费用;若不能,请说明理由.
某运输部门规定:办理托运,当一种物品的重量不超过16千克时,需付基础费30元和保险费a元:为限制过重物品的托运,当一件物品超过16千克时,除了付以上基础费和保险费外,超过部分每千克还需付b元超重费.设某件物品的重量为x千克.
(1)当x≤16时,支付费用为a+30元(用含a的代数式表示);当x≥16时,支付费用为a+30+(x-16)b元(用含x和a、b的代数式表示);
(2)甲、乙两人各托运一件物晶,物品重量和支付费用如下表所示
| 物品重量(千克) | 支付费用(元) |
| 18 | 38 |
| 25 | 53 |
②试问在物品可拆分的情况下,用不超过105元的费用能否托运50千克物品?若能,请设计出其中一种托运方案,并求出托运费用;若不能,请说明理由.
17.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后获毛利润共2.1万元(毛利润=(售价-进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量,已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,设甲种手机减少x部,求y的解析式.
(3)该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
| 甲 | 乙 | |
| 进价(元/部) | 4000 | 2500 |
| 售价(元/部) | 4300 | 3000 |
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量,已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,设甲种手机减少x部,求y的解析式.
(3)该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
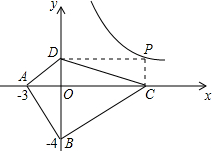 如图,已知A(-3,0),B(0,-4),P为双曲线y=$\frac{12}{x}$(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.则四边形ABCD面积的最小值为24.
如图,已知A(-3,0),B(0,-4),P为双曲线y=$\frac{12}{x}$(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.则四边形ABCD面积的最小值为24.