题目内容
18．已知A（0，1）、B（4．-1）、C（7，5）、D（3，7）四点的坐标，求证：四边形ABCD是矩形．分析 由勾股定理求出AB、BC、CD、AD，证出四边形ABCD是平行四边形，再由勾股定理的逆定理证出直角，即可得出结论．
解答 解：如图所示：
∵A（0，1）、B（4．-1）、C（7，5）、D（3，7），
∴AB2=42+22=20，BC2=62+32=45，CD2=42+22=20，AD2=62+32=45，
∴AB=CD，AD=BC，
∴四边形ABCD是平行四边形，
∵AC2=72+42=65=AB2+BC2，
∴∠ABC=90°，
∴四边形ABCD是矩形．
点评 本题考查了矩形的判定、平行四边形的判定、坐标与图形性质、勾股定理；熟练掌握矩形的判定，由勾股定理求出直角是解决问题的关键．
练习册系列答案
相关题目
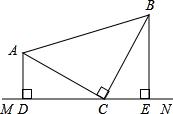已知：在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．试猜想AD与CE的大小关系并说明理由．
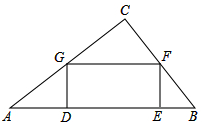如图，在直角三角形ABC中，∠C=90°，AC=3，BC=4，矩形DEFG内接于△ABC中，如果DG：DE=3：5，求矩形DEFG的周长．
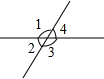如图，如果∠1=120°，则∠2=60°．