Question

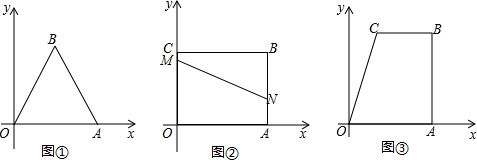
15．问题探究
（1）如图①，边长为4的等边△OAB位于平面直角坐标系中，将△OAB沿过P（2，$\sqrt{3}}$）的直线折叠，使点B落在x轴上，则B的对应点B'有1个，其坐标为（2，0）；
（2）如图②，长方形OABC位于平面直角坐标系中，其中OA=8，AB=6．将长方形OABC沿过P（8，2）的直线折叠，使点B落在x轴上，则B的对应点B'的坐标为（8-2$\sqrt{3}$，0）或（8+2$\sqrt{3}$，0）．
问题解决
（3）如图③，四边形OABC位于平面直角坐标系中，其中OA=AB=8，BC=4，BC∥OA，AB⊥OA于点A．将四边形OABC沿过P（5，3）的直线折叠，使点B落在x轴上，问是否存在过点P且与线段OC相交的折痕，若存在，求出折痕与OC的交点坐标；若不存在，请说明理由．

Answer 1

分析 （1）如图1中，作BH⊥OA于H．只要证明点P在线段BH上，且PB=PH=$\sqrt{3}$，由此得出结论点B′与点H重合，即可解决问题．
（2）如图2中，点B的对应点有B′和B″两个，分别利用勾股定理即可解决问题．
（3）存在．求出直线OC的解析式，再求出折痕的解析式，利用方程组即可解决问题．

解答 解：（1）如图1中，作BH⊥OA于H．

∵△ABC是等边三角形，OA=OB=AB=4，
∴OH=AH=2，BH=OH•tan60°=2$\sqrt{3}$，
∵P（2，$\sqrt{3}$），
∴点P在线段PH上，且PB=PH，
∵将△OAB沿过P（2，$\sqrt{3}}$）的直线折叠，使点B落在x轴上，
∴PB=PB′，
∴点B′与点H重合，
∴B′（2，0），
故答案为1，（2，0）；

（2）如图2中，点B的对应点有B′和B″两个，

∵PB=PB′=PB″=4，
在Rt△PAB′和Rt△PAB″中，AB′=AB″=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$，
∴B′（8-2$\sqrt{3}$，0），B″（8+2$\sqrt{3}$，0）；
故答案为（8-2$\sqrt{3}$，0）或（8+2$\sqrt{3}$，0）；

（3）存在．理由如下：
如图3中，点B的对应点有B′和B″两个，作PE⊥AB于E，PF⊥OA于F．

∵P（5，3），
∴PF=3，OF=5，AF=PE=AE=3，BE=5，
∵PB=PB′=PB″，PE=PF，
∴△PBE≌△PB′F≌△PB″F，
∴FB′=FB″=EB=5，
∴B′与O重合，B″（10，0），
∵C（4，8），
∴直线OC的解析式为y=2x，
∵B（8，8），
∴直线OB的解析式为y=x，设折痕与OC交于点G，与BB′交于点H，
∵H（4，4），
∴直线GH的解析式为y=-x+8，
由$\left\{\begin{array}{l}{y=2x}\\{y=-x+8}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{8}{3}}\\{y=\frac{16}{3}}\end{array}\right.$，
∴折痕GH与OC的交点G坐标（$\frac{8}{3}$，$\frac{16}{3}$），
∵B（8，8），B″（10，0），
∴直线BB″的解析式为y=-4x+40，设折痕与OC交于点N，与BB″交于点M，
∵M（9，4），
∴直线MN的解析式为y=$\frac{1}{4}$x+$\frac{7}{4}$，
由$\left\{\begin{array}{l}{y=2x}\\{y=\frac{1}{4}x+\frac{7}{4}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$，
∴折痕MN与OC的交点N坐标为（1，2）．
综上所述，折痕与OC的交点坐标为（$\frac{8}{3}$，$\frac{16}{3}$）或（1，2）；

点评 本题考查几何变换、等边三角形的性质，矩形的性质，勾股定理、一次函数的应用等知识，解题的关键是学会构建一次函数，利用方程组求两个函数的交点坐标，属于中考压轴题．