题目内容
18.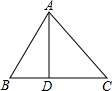 如图,△ABC中,AB=12,BC=15,AD⊥BC于点D,∠BAD=30°,求tanC的值.
如图,△ABC中,AB=12,BC=15,AD⊥BC于点D,∠BAD=30°,求tanC的值.
分析 根据在△ABC中,AB=12,BC=15,AD⊥BC于点D,∠BAD=30°,可以求得BD、AD、CD的长,从而可以求得tanC的值.
解答 解:∵△ABC中,AB=12,BC=15,AD⊥BC于点D,∠BAD=30°,
∴∠ADB=∠ADC=90°,
∴AB=2BD,
∴BD=6,
∴CD=BC-BD=15-6=9,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}=\sqrt{1{2}^{2}-{6}^{2}}=6\sqrt{3}$,
∴tanC=$\frac{AD}{CD}=\frac{6\sqrt{3}}{9}=\frac{2\sqrt{3}}{3}$.
即tanC的值是$\frac{2\sqrt{3}}{3}$.
点评 本题考查解直角三角形,解题的关键是计算出题目中各边的长,找出所求问题需要的条件.

练习册系列答案
相关题目
8. 为了解我省2015届九年级学生学业水平考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:0-29分;B:30-39分;C:40-44分;D:45-49分;E:50分)统计如下:
为了解我省2015届九年级学生学业水平考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:0-29分;B:30-39分;C:40-44分;D:45-49分;E:50分)统计如下:
学业考试体育成绩(分数段)统计表
根据上面提供的信息,回答下列问题:
(1)在统计表中,a的值为60,b的值为0.15,并将统计图补充完整;
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数.”请问:甲同学的体育成绩应在什么分数段内?C(填相应分数段的字母).
(3)如果把成绩在45分以上(含45分)定为优秀,那么该县2015年4020名九年级学生中体育成绩为优秀的学生人数约有多少名?
 为了解我省2015届九年级学生学业水平考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:0-29分;B:30-39分;C:40-44分;D:45-49分;E:50分)统计如下:
为了解我省2015届九年级学生学业水平考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:0-29分;B:30-39分;C:40-44分;D:45-49分;E:50分)统计如下:学业考试体育成绩(分数段)统计表
| 分数段 | 人数(人) | 频率 |
| A | 12 | 0.05 |
| B | 36 | b |
| C | 84 | 0.35 |
| D | a | 0.25 |
| E | 48 | 0.2 |
(1)在统计表中,a的值为60,b的值为0.15,并将统计图补充完整;
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数.”请问:甲同学的体育成绩应在什么分数段内?C(填相应分数段的字母).
(3)如果把成绩在45分以上(含45分)定为优秀,那么该县2015年4020名九年级学生中体育成绩为优秀的学生人数约有多少名?
9. 如图,⊙O是△ABC的外接圆,∠BOC=110°,则∠A的度数为( )
如图,⊙O是△ABC的外接圆,∠BOC=110°,则∠A的度数为( )
 如图,⊙O是△ABC的外接圆,∠BOC=110°,则∠A的度数为( )
如图,⊙O是△ABC的外接圆,∠BOC=110°,则∠A的度数为( )| A. | 110° | B. | 60° | C. | 55° | D. | 50° |
6.如果分式$\frac{|x|-1}{2x+2}$的值为0,则x的值是( )
| A. | 1 | B. | 0 | C. | -1 | D. | ±1 |
13.下列运算正确的是( )
| A. | 3x+4y=7xy | B. | 6y2-y2=5 | C. | b4+b3=b7 | D. | 4x-x=3x |