题目内容
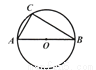
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,AB=8.
(1)利用尺规,作∠CAB的平分线,交⊙O于点D;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接CD,OD,若AC=CD,求∠B的度数;
(3)在(2)的条件下,OD交BC于点E.求出由线段ED,BE,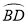 所围成区域的面积.(其中
所围成区域的面积.(其中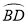 表示劣弧,结果保留π和根号)
表示劣弧,结果保留π和根号)
练习册系列答案
相关题目
题目内容
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,AB=8.
(1)利用尺规,作∠CAB的平分线,交⊙O于点D;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接CD,OD,若AC=CD,求∠B的度数;
(3)在(2)的条件下,OD交BC于点E.求出由线段ED,BE,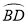 所围成区域的面积.(其中
所围成区域的面积.(其中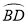 表示劣弧,结果保留π和根号)
表示劣弧,结果保留π和根号)
