题目内容
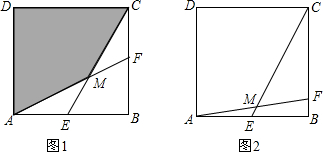
 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,若∠B=62°,则∠E=( )
如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,若∠B=62°,则∠E=( )| A、30° | B、31° |
| C、32° | D、36° |
考点:线段垂直平分线的性质
专题:
分析:根据线段垂直平分线性质得出AB=AC,AC=CE,推出∠B=∠ACB=62°,∠E=∠CAE,根据三角形外角性质得出即可.
解答:解:∵AD⊥BC,BD=DC,
∴AB=AC,
∴∠B=∠ACB,
∵∠B=62°,
∴∠ACB=62°,
∵点C在AE的垂直平分线上,
∴AC=CE,
∴∠E=∠CAE,
∵∠E+∠CAE=∠ACB=62°,
∴∠E=31°,
故选B.
∴AB=AC,
∴∠B=∠ACB,
∵∠B=62°,
∴∠ACB=62°,
∵点C在AE的垂直平分线上,
∴AC=CE,
∴∠E=∠CAE,
∵∠E+∠CAE=∠ACB=62°,
∴∠E=31°,
故选B.
点评:本题考查了等腰三角形的性质,三角形外角的性质,线段垂直平分线性质的应用,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
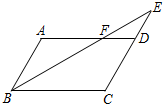 如图,在?ABCD中,E是CD的延长线上一点,BE与AD交于点F,若CD=2DE,则AF:FD的值为( )
如图,在?ABCD中,E是CD的延长线上一点,BE与AD交于点F,若CD=2DE,则AF:FD的值为( )| A、3:2 | B、2:3 |
| C、2:1 | D、3:1 |
 如图,PQ是⊙O1,⊙O2的公共弦,过点P的直线分别交⊙O1,⊙O2于点A、D,过点Q的直线分别交⊙O1,⊙O2于点B、C,则下列结论不一定成立的是( )
如图,PQ是⊙O1,⊙O2的公共弦,过点P的直线分别交⊙O1,⊙O2于点A、D,过点Q的直线分别交⊙O1,⊙O2于点B、C,则下列结论不一定成立的是( )| A、AB∥CD |
| B、∠ABQ=∠DPQ |
| C、∠PAB+∠PQB=180° |
| D、AD∥BC |
 如图,AD平分∠BAC,DE∥AC交AB于点E,∠1=25°,则∠BED等于( )
如图,AD平分∠BAC,DE∥AC交AB于点E,∠1=25°,则∠BED等于( )| A、40° | B、50° |
| C、60° | D、25° |
下列式子中,属于最简二次根式的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列四个数中最小的是( )
| A、|-3| | ||
| B、30 | ||
C、(
| ||
| D、(-3)5 |