题目内容
【题目】综合与探究:
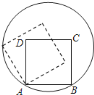
(1)操作发现:如图1,在![]() 中,
中,![]() 为锐角,
为锐角,![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() ,以
,以![]() 为直角边且在
为直角边且在![]() 的上方作等腰直角三角形
的上方作等腰直角三角形![]() .若
.若![]() ,
,![]() .当点
.当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),你能发现
不重合),你能发现![]() 与
与![]() 的数量关系和位置关系吗?请直接写出你发现的结论.
的数量关系和位置关系吗?请直接写出你发现的结论.

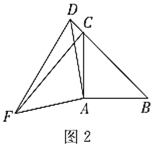
(2)类比与猜想:当点![]() 在线段
在线段![]() 的延长线上时,其余条件不变,(1)中的结论是否仍然成立?请在图2中画出相应图形并说明理由.
的延长线上时,其余条件不变,(1)中的结论是否仍然成立?请在图2中画出相应图形并说明理由.

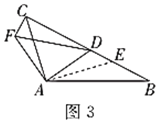
(3)深入探究:如图3,若![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动,请写出
上运动,请写出![]() 与
与![]() 的位置关系并证明.
的位置关系并证明.

【答案】(1)![]() ,
,![]() .(2)成立,证明见解析;(3)
.(2)成立,证明见解析;(3)![]() .证明见解析
.证明见解析
【解析】
(1)根据同角的余角相等求出∠CAF=∠BAD,然后利用“边角边”证明△ACF和△ABD全等,
(2)先求出∠CAF=∠BAD,然后与(1)的思路相同求解即可;
(3)过点A作AE⊥AC交BC于E,可得△ACE是等腰直角三角形,根据等腰直角三角形的性质可得AC=AE,∠AED=45°,再根据同角的余角相等求出∠CAF=∠EAD,然后利用“边角边”证明△ACF和△AED全等,根据全等三角形对应角相等可得∠ACF=∠AED,然后求出∠BCF=90°,从而得到CF⊥BD.
解:∵![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)成立.
证明:如图2,
∵![]() ,
,
∴![]() ,
,
即![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)![]() .
.
证明:如图3,过点![]() 作
作![]() 交
交![]() 于
于![]() .
.
∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

【题目】某公司根据市场计划调整投资策略,对![]() ,
,![]() 两种产品进行市场调查,收集数据如表:
两种产品进行市场调查,收集数据如表:
项目 产品 | 年固定成本 (单位:万元) | 每件成本 (单位:万元) | 每件产品销售价 (万元) | 每年最多可生产的件数 |
|
|
|
|
|
|
|
|
|
|
其中![]() 是待定常数,其值是由生产
是待定常数,其值是由生产![]() 的材料的市场价格决定的,变化范围是
的材料的市场价格决定的,变化范围是![]() ,销售
,销售![]() 产品时需缴纳
产品时需缴纳![]() 万元的关税,其中
万元的关税,其中![]() 为生产产品的件数,假定所有产品都能在当年售出,设生产
为生产产品的件数,假定所有产品都能在当年售出,设生产![]() ,
,![]() 两种产品的年利润分别为
两种产品的年利润分别为![]() 、
、![]() (万元),写出
(万元),写出![]() 、
、![]() 与
与![]() 之间的函数关系式,注明其自变量
之间的函数关系式,注明其自变量![]() 的取值范围.
的取值范围.
【题目】国家实行一系列“三农”优惠政策后,农民收入大幅度增加.某乡所辖村庄去年的年人均收入(单位:元)情况如下表:
年人均收入 | 3 500 | 3 700 | 3 800 | 3 900 | 4 500 |
村庄个数 | 1 | 1 | 3 | 3 | 1 |
该乡去年各村庄年人均收入的中位数是( )
A.3 700元B.3 800元C.3 850元D.3 900元