题目内容
7. 如图,四边形ABCD和AEFG均为正方形,则DG:CF:BE=1:$\sqrt{2}$:1.
如图,四边形ABCD和AEFG均为正方形,则DG:CF:BE=1:$\sqrt{2}$:1.
分析 连结EG交AB于O,如图,根据正方形的性质得GE⊥AF,AG=AE,OA=OE=OF,则可证明△ADG≌△ABE得到DG=BE,接着设OA=OF=OE=x,AB=BC=a,则BF=a-2x,利用勾股定理可表示出BE2=2x2-2ax+a2,CF2=4x2-2ax+2a2,于是得到CF=$\sqrt{2}$BE,所以DG:CF:BE=1:$\sqrt{2}$:1.
解答 解: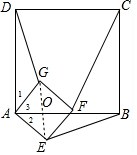 连结EG交AB于O,如图,
连结EG交AB于O,如图,
∵四边形AEFG为正方形,
∴GE⊥AF,AG=AE,OA=OE=OF,
∵四边形ABCD为正方形,
∴AB=AD=BC,
∵∠1+∠3=90°,∠2+∠3=90°,
∴∠1=∠2,
在△ADG和△ABE中
$\left\{\begin{array}{l}{AD=AB}\\{∠1=∠2}\\{AG=AE}\end{array}\right.$,
∴△ADG≌△ABE,
∴DG=BE,
设OA=OF=OE=x,AB=BC=a,则BF=a-2x,
在Rt△BEO中,BE2=OE2+BO2=x2+(a-x)2=2x2-2ax+a2,
在Rt△BCF中,CF2=BC2+BF2=a2+(a-2x)2=4x2-2ax+2a2,
∴CF2=2BE2,
∴CF=$\sqrt{2}$BE,
∴DG:CF:BE=1:$\sqrt{2}$:1.
故答案为1:$\sqrt{2}$:1.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.利用三角形全等是证明线段相等的常用方法.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
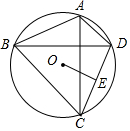 如图,圆O中,弦AC⊥BD,且OE⊥CD于E,若AB的长是10,则OE的长是5.
如图,圆O中,弦AC⊥BD,且OE⊥CD于E,若AB的长是10,则OE的长是5. 如图:有一个圆柱,底面圆的直径AB=$\frac{16}{π}$,高BC=12,P为BC的中点,蚂蚁从A点爬到P点的最短距离是10.
如图:有一个圆柱,底面圆的直径AB=$\frac{16}{π}$,高BC=12,P为BC的中点,蚂蚁从A点爬到P点的最短距离是10.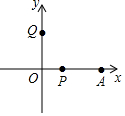 如图,在平面直角坐标系中有一点A,OA=16,动点P从A开始以每秒2个单位的速度向x轴负半轴运动,动点Q从0开始以每秒1个单位的速度向y轴正半轴运动,P,Q同时出发,设时间为t;
如图,在平面直角坐标系中有一点A,OA=16,动点P从A开始以每秒2个单位的速度向x轴负半轴运动,动点Q从0开始以每秒1个单位的速度向y轴正半轴运动,P,Q同时出发,设时间为t;