题目内容
如图，在等腰三角形ACB中，AC=BC=5，AB=8，D为底边AB上一动点（不与点A，B重合），DE⊥AC，DF⊥BC，垂足分别为E，F，求DE+DF的长．考点：等腰三角形的性质
专题：
分析：连接CD，过C点作底边AB上的高CG，根据S△ABC=S△ACD+S△DCB不难求得DE+DF的值．
解答：
解：连接CD，过C点作底边AB上的高CG，
∵AC=BC=5，AB=8，
∴BG=4，CG=
=
=3，
∵S△ABC=S△ACD+S△DCB，
∴AB•CG=AC•DE+BC•DF，
∵AC=BC，
∴8×3=5×（DE+DF）
∴DE+DF=4.8．
故答案为：4.8．
解：连接CD，过C点作底边AB上的高CG，∵AC=BC=5，AB=8，
∴BG=4，CG=
| BC2-BG2 |
| 52-42 |
∵S△ABC=S△ACD+S△DCB，
∴AB•CG=AC•DE+BC•DF，
∵AC=BC，
∴8×3=5×（DE+DF）
∴DE+DF=4.8．
故答案为：4.8．
点评：本题考查了等腰三角形的性质，辅助线是解决几何问题的一个关键，此外此题还考查了等腰三角形“三线合一”的性质．
练习册系列答案
相关题目
和频数分布直方图．
星期天，小华到小明家邀请小明到新华书店看书，当小华到达CD（点D是小华的眼睛）处时，发现小明在七楼A处，此时测得仰角为45°，然后他向前走了10m到达C′D′处，发现小明在六楼B处，此时测得仰角为60°，已知楼层高AB=2.7m，求C′D′处到楼脚O点的距离．（参考数据：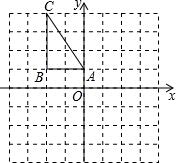
如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（0，1），B（-2，1），C（-2，4）．