题目内容
5.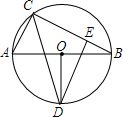 已知:如图,在⊙O中,AB是直径,OD⊥AB,连接CD,过D作DE垂直于BC于E,AB=8,CD=6,求BE的长.
已知:如图,在⊙O中,AB是直径,OD⊥AB,连接CD,过D作DE垂直于BC于E,AB=8,CD=6,求BE的长.
分析 连结DA、DB,如图,根据垂径定理得到$\widehat{AD}$=$\widehat{BD}$,则DA=DB,∠DCA=∠DCB,再利用圆周角定理得∠ACB=∠ADB=90°,所以△ADB为等腰直角三角形,∠DCB=45°,则利用等腰直角三角形的性质可计算出DE=$\frac{\sqrt{2}}{2}$CD=3$\sqrt{2}$,DB=$\frac{\sqrt{2}}{2}$AB=4$\sqrt{2}$,然后在Rt△BDE中利用勾股定理可计算出BE.
解答 解:连结DA、DB,如图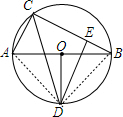 ,
,
∵OD⊥AB,
∴$\widehat{AD}$=$\widehat{BD}$,
∴DA=DB,∠DCA=∠DCB,
∵AB为直径,
∴∠ACB=∠ADB=90°,
∴△ADB为等腰直角三角形,∠DCB=45°,
∴DE=$\frac{\sqrt{2}}{2}$CD=3$\sqrt{2}$,DB=$\frac{\sqrt{2}}{2}$AB=4$\sqrt{2}$,
在Rt△BDE中,BE=$\sqrt{B{D}^{2}-D{E}^{2}}$=$\sqrt{(4\sqrt{2})^{2}-(3\sqrt{2})^{2}}$=$\sqrt{14}$.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.本题的关键是判断△ADB和△CDE为等腰直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目