题目内容
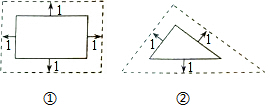
12.在研究相似问题时,甲、乙同学的观点如下:甲:将邻边边长为5和8的矩形按图①的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
乙:将边长5、12、13的三角形按图②的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
对于两人的观点,下列说法正确的是( )
| A. | 两人都对 | B. | 两人都不对 | C. | 甲对、乙不对 | D. | 甲不对,乙对 |
分析 利用位似图形的性质以及相似多边形的判定方法得出即可.
解答 解:由题意可得新矩形边长为:7和10,
$\frac{5}{8}$≠$\frac{7}{10}$,
故两矩形不相似,
当新三角形的对应边间距离均为1时,则两三角形的对应边平行,且对应点连线相交于一点,故两三角形位似,即相似,
故选:D.
点评 此题主要考查了相似三角形以及相似多边形的判定,熟练应用相似多边形的判定方法是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列运算不能用平方差公式的是( )
| A. | (a-b)(-b-a) | B. | (m2-n2)(n2+m2) | C. | (1-3a)(3a+1) | D. | (a+b)(-a-b) |
7.关于方程x2-2=0的理解错误的是( )
| A. | 这个方程是一元二次方程 | |
| B. | 方程的解是$\sqrt{2}$ | |
| C. | 这个方程可以化成一元二次方程的一般形式 | |
| D. | 这个方程可以用公式法求解 |
4. 如图,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF的度数为( )
如图,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF的度数为( )
 如图,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF的度数为( )
如图,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF的度数为( )| A. | 100° | B. | 120° | C. | 115° | D. | 130° |
1.下列根式中与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{12}$ | C. | $\sqrt{18}$ | D. | $\sqrt{\frac{2}{3}}$ |

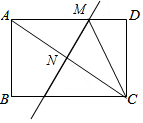 如图,在长方形ABCD中,AB=3,BC=6,对角线AC的垂直平分线分别交AD、AC于点M,N,连接CM,则CM的长为$\frac{15}{4}$.
如图,在长方形ABCD中,AB=3,BC=6,对角线AC的垂直平分线分别交AD、AC于点M,N,连接CM,则CM的长为$\frac{15}{4}$.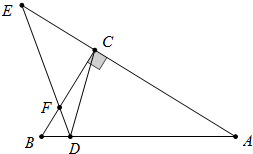 △ABC中,∠ACB=90°,AD=AC,∠CDE=45°,若BD=1,EF=2$\sqrt{5}$,则AD的长为4.
△ABC中,∠ACB=90°,AD=AC,∠CDE=45°,若BD=1,EF=2$\sqrt{5}$,则AD的长为4.