题目内容
20.用长为32米的篱笆围一个矩形养鸡场,设围成的矩形一边长为x米,面积为y平方米.(1)求y关于x的函数关系式;并写出x的取值范围.
(2)当x为何值时,围成的养鸡场面积为60平方米?
(3)能否围成面积为70平方米的养鸡场?如果能,请求出其边长;如果不能,请说明理由.
分析 (1)根据矩形的面积公式进行列式;
(2)、(3)把y的值代入(1)中的函数关系,求得相应的x值即可.
解答 解:(1)y=x(16-x)=-x2+16x,( 0<x<16).
(2)当y=60时,-x2+16x=60,解得 x1=10,x2=6
所以当x=10或6时,围成的养鸡场的面积为60平方米.
(3)当y=70时,-x2+16x=70,整理得:x2-16x+70=0,
由于△=256-280=-24<0
所以此方程无解,不能围成面积为70的养鸡场.
点评 本题考查了一元二次方程的应用,解题的关键是熟悉矩形的周长与面积的求法,以及一元二次方程的根的判别式,属于基础题中考常考题型.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
12.在研究相似问题时,甲、乙同学的观点如下:
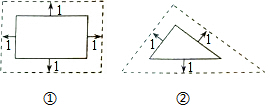
甲:将邻边边长为5和8的矩形按图①的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
乙:将边长5、12、13的三角形按图②的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
对于两人的观点,下列说法正确的是( )
甲:将邻边边长为5和8的矩形按图①的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
乙:将边长5、12、13的三角形按图②的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
对于两人的观点,下列说法正确的是( )

| A. | 两人都对 | B. | 两人都不对 | C. | 甲对、乙不对 | D. | 甲不对,乙对 |
9.下列运算正确的是( )
| A. | 4a2-2a2=2 | B. | (a2)3=a6 | C. | a2a3=a6 | D. | a3+a2=a5 |