题目内容
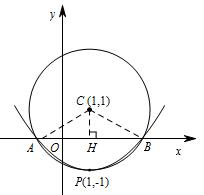
如图,在平面直角坐标系中,以点C(1,1) 为圆心,2 为半径作圆,交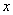 轴于A,B 两点,点 P在 ⊙C上.
轴于A,B 两点,点 P在 ⊙C上.
(1) 求出A,B 两点的坐标;
(2) 试确定经过 A、 B两点且以点 P为顶点的抛物线解析式;
(3) 在该抛物线上是否存在一点D,使线段 OP与CD 互相平分?若存在,求出点 D 的坐标;若不存在,请说明理由.
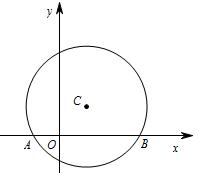 |
解:(1) 做CH⊥x轴,H 为垂足,连接CB-----------1分
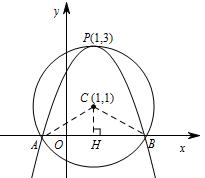 ∵CH=1,半径CB=2
∵CH=1,半径CB=2
∴HB=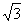 -------------------------------------2分
-------------------------------------2分
故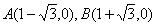 -----------------------3分
-----------------------3分
(2) 由圆与抛物线的对称性可知抛物线的顶点P 的坐标为
(1,3) 或(1,-1)---------------------------------4分
情况一:设抛物线表达式y=a(x-1)2+3,
 把点
把点 代入上式,解得a=-1.
代入上式,解得a=-1.
∴ y=-x2+2x+2-----------------------------------5分
情况二:设抛物线解析式y=a(x-1)2-1,
把点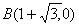 代入上式,解得
代入上式,解得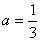 ,
,
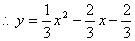 ------------------------------6分
------------------------------6分
(3) 假设存在点D 使线段OP 与CD 互相平分,
则四边形OCPD 是平行四边形-
∴PC∥OD且PC=OD
∵PC∥Y轴
∴点D在Y轴上.
又PC=2,
∴OD=2,即D(0,2) 或(0,-2) -
(0,2) 满足y=-x2+2x+2
(0,-2) 不满足任何一条抛物线的解析式,
∴ 点D(0,2) 在抛物线上.
所以存在D(0,2) 使线段OP 与CD 互相平分

练习册系列答案
相关题目
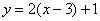 的对称轴是 .
的对称轴是 .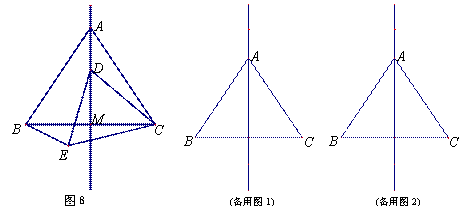 (3)当动点D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.
(3)当动点D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由. ,则
,则 的值为_____.
的值为_____.
 的结果是( ).
的结果是( ). B.
B. C.4 D.
C.4 D.
 ,那么袋中的球共有__________个.
,那么袋中的球共有__________个.