题目内容
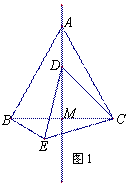
如图8所示,在等边△ABC中,线段AM为BC边上的中线. 动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)填空:∠CAM= 度;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
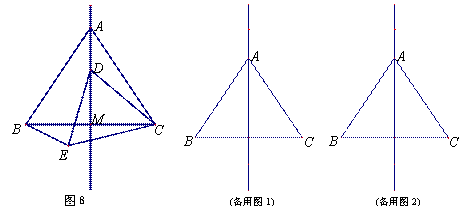 (3)当动点D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.
(3)当动点D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.
解: (1)30;………………………………………………………..1分
(2)∵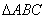 与
与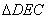 都是等边三角形
都是等边三角形
∴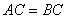 ,
,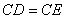 ,
,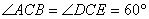 ……………….2分
……………….2分
∴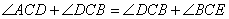
 ∴
∴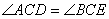
∴ ≌
≌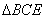
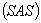 …………………………………………...3分
…………………………………………...3分
(3) 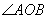 是定值,
是定值,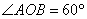 ,理由如下:
,理由如下:
①当点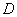 在线段
在线段 上时,如图1,由(2)可知
上时,如图1,由(2)可知 ≌
≌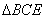 ,
,
则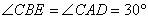 ,又
,又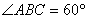
∴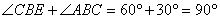 ………………………..............4分
………………………..............4分
 ∵
∵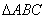 是等边三角形,线段
是等边三角形,线段 为
为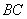 边上的中线
边上的中线
∴ 平分
平分 ,即
,即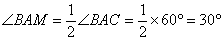
∴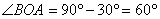 ………………………………5分
………………………………5分
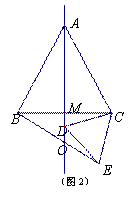
②当点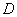 在线段
在线段 的延长线上时,如图2,
的延长线上时,如图2,
∵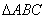 与
与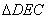 都是等边三角形
都是等边三角形
∴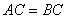 ,
,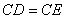 ,
,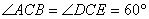
∴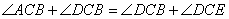 ,∴
,∴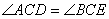
∴ ≌
≌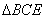
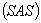 ………………………………...6分
………………………………...6分
∴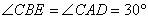 ,同理可得:
,同理可得: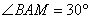 ,∴
,∴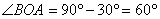 …………………………………….7分
…………………………………….7分
 ③当点
③当点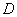 在线段
在线段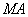 的延长线上时,
的延长线上时,
∵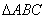 与
与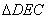 都是等边三角形
都是等边三角形
∴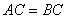 ,
,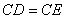 ,
,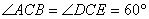
∴
∴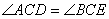
∴ ≌
≌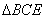
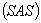 ……………………………….8分
……………………………….8分
∴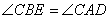
同理可得: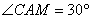
∴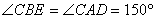
∴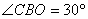 ,
,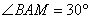 ,∴
,∴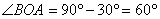 ……………9分
……………9分

练习册系列答案
相关题目
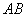 是⊙
是⊙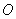 的直径,
的直径, 是⊙
是⊙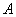 为切点,
为切点,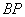 与⊙
与⊙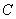 ,点
,点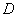 是
是 .
.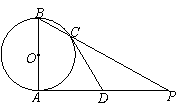 (1)证明:
(1)证明: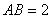 ,
,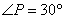 ,求
,求 ◆
◆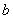 =
=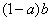 ,下面给出了关于这种运算的四个结论:
,下面给出了关于这种运算的四个结论: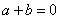 ,则(
,则(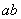
 有一根为0,则
有一根为0,则 的值是
的值是 D. 0
D. 0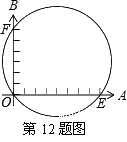 A.10个单位
A.10个单位  轴于A,B 两点,点 P在 ⊙C上.
轴于A,B 两点,点 P在 ⊙C上.