题目内容
 如图,在△ABC中,∠B=2∠C,AD⊥BC于D,M为BC的中点,求证:DM=
如图,在△ABC中,∠B=2∠C,AD⊥BC于D,M为BC的中点,求证:DM=| 1 |
| 2 |
考点:三角形中位线定理,等腰三角形的判定与性质
专题:证明题
分析:取AC的中点N,连接MN,DN,由M为BC的中点,得到MN为三角形ABC的中位线,利用中位线定理得到MN等于AB的一半,且MN与AB平行,由两直线平行同位角相等得到∠NMC=∠B,而∠B=2∠C,等量代换得到∠NMC=2∠C,而DN为直角三角形ADC斜边上的中线,得到DN=NC,等边对等角得到∠MDN=∠C,又∠NMC为三角形DMN的外角,利用三角形的外角性质及等量代换可得出∠MDN=∠MND,利用等角对等边可得出DM=MN,等量代换即可得证.
解答: 证明:取AC的中点N,连接MN,DN,
证明:取AC的中点N,连接MN,DN,
∵M为BC的中点,
∴MN为△ABC的中位线,
∴MN∥AB,且MN=
AB,
∴∠B=∠NMC,又∠B=2∠C,
∴∠NMC=2∠C,
∵∠NMC为△DMN的外角,
∴∠NMC=∠MDN+∠MND=2∠C,
又DN为Rt△ADC斜边上的中线,
∴DN=NC=AN=
AC,
∴∠MDN=∠C,
∴∠MND=∠C=∠MDN,
∴DM=MN,
则DM=
AB.
 证明:取AC的中点N,连接MN,DN,
证明:取AC的中点N,连接MN,DN,∵M为BC的中点,
∴MN为△ABC的中位线,
∴MN∥AB,且MN=
| 1 |
| 2 |
∴∠B=∠NMC,又∠B=2∠C,
∴∠NMC=2∠C,
∵∠NMC为△DMN的外角,
∴∠NMC=∠MDN+∠MND=2∠C,
又DN为Rt△ADC斜边上的中线,
∴DN=NC=AN=
| 1 |
| 2 |
∴∠MDN=∠C,
∴∠MND=∠C=∠MDN,
∴DM=MN,
则DM=
| 1 |
| 2 |
点评:此题考查了等腰三角形的判定与性质,三角形的中位线定理,三角形的外角性质,以及平行线的判定与性质,熟练掌握等腰三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
下列方程中,是一元一次方程的是( )
| A、x+y=1 | ||
| B、x2-x=1 | ||
C、
| ||
D、
|
下列语句是真命题的是( )
| A、大于锐角的角是钝角 |
| B、如果一个实数有算术平方根,那么它的算术平方根是整数 |
| C、如果AC=BC,那么点C是线段AB的中点 |
| D、在同一平面,内错角相等,两直线平行 |
已知x=2是方程x2-6x+m=0的根,则该方程的另一根为( )
| A、2 | B、3 | C、4 | D、8 |
下列等式一定成立的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、(
|
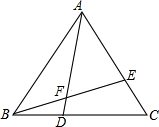 如图,在等边△ABC中,点D、E分别是边BC、AC上的点,且BD=CE,连接BE、AD,相交于点F.
如图,在等边△ABC中,点D、E分别是边BC、AC上的点,且BD=CE,连接BE、AD,相交于点F. 如图,已知点O在直线AB上,OM平分∠AOC,ON平分∠COB,∠NOB=65°
如图,已知点O在直线AB上,OM平分∠AOC,ON平分∠COB,∠NOB=65°