题目内容
8.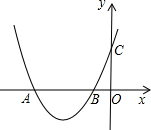 如图,抛物线y=ax2+bx+c与x轴相交于A、B两点,与y轴相交于点C,若OA=2OC,判断a、b、c之间的关系.
如图,抛物线y=ax2+bx+c与x轴相交于A、B两点,与y轴相交于点C,若OA=2OC,判断a、b、c之间的关系.
分析 假设C点坐标为(0,m),根据OA=2OC得出A(-2m,0),代入解析式即可得出a、b、c之间的关系.
解答 解:设C点坐标为(0,m),
∵OA=2O2,
∴A(-2,0),
把A、C点坐标代入解析式得,
∴0=4am2-2mb+c,
∴m=c,
∵4ac2-2bc+c=0,
由图象可知c≠0,两边同时除以c得,
∴2ac-2b+1=0,
∴ac=b-$\frac{1}{2}$.
点评 此题主要考查了二次函数图象和系数的关系,得出图象上两点的坐标进而表示出a,b,c的关系是解决问题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
6.用给定长度的绳子围成下面四种几何图形,其面积一定最大的是( )
| A. | 三角形 | B. | 平行四边形 | C. | 正方形 | D. | 菱形 |
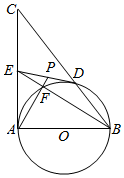 如图,在△ABC中,∠BAC=90°,E是AC的中点,AB是⊙O的直径,⊙O交BC于点D,BE交⊙O于点F,连接AF,AF的延长线交DE于点P.
如图,在△ABC中,∠BAC=90°,E是AC的中点,AB是⊙O的直径,⊙O交BC于点D,BE交⊙O于点F,连接AF,AF的延长线交DE于点P.