题目内容
11. 如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )| A. | ($\frac{2}{3}$,3),(-$\frac{1}{2}$,4) | B. | ($\frac{7}{4}$,$\frac{7}{2}$),($-\frac{1}{2}$,4) | C. | ($\frac{2}{3}$,3),($-\frac{2}{3}$,4) | D. | ($\frac{7}{4}$,$\frac{7}{2}$),($-\frac{2}{3}$,4) |
分析 先过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,过点C作CF∥y轴,过点A作AF∥x轴,交点为F,易得△CAF≌△BOE,△AOD∽△OBE,然后由相似三角形的对应边成比例求得答案.
解答 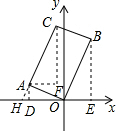 解:如图,过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,过点C作CF∥y轴,过点A作AF∥x轴,交点为F,延长CA交x轴于点H,
解:如图,过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,过点C作CF∥y轴,过点A作AF∥x轴,交点为F,延长CA交x轴于点H,
∵四边形AOBC是矩形,
∴AC∥OB,AC=OB,
∴∠CAF=∠BOE=∠CHO,
在△ACF和△OBE中,
$\left\{\begin{array}{l}{∠F=∠BEO=90°}\\{∠CAF=∠BOE}\\{AC=OB}\end{array}\right.$,
∴△CAF≌△BOE(AAS),
∴BE=CF=4-1=3,
∵∠AOD+∠BOE=∠BOE+∠OBE=90°,
∴∠AOD=∠OBE,
∵∠ADO=∠OEB=90°,
∴△AOD∽△OBE,
∴$\frac{AD}{OE}$=$\frac{OD}{BE}$,
即$\frac{1}{OE}$=$\frac{2}{3}$,
∴OE=$\frac{3}{2}$,即点B($\frac{3}{2}$,3),
∴AF=OE=$\frac{3}{2}$,
∴点C的横坐标为:-(2-$\frac{3}{2}$)=-$\frac{1}{2}$,
∴点C(-$\frac{1}{2}$,4).
故选:A.
点评 此题考查了矩形的性质、全等三角形的判定与性质以及相似三角形的判定与性质.此题注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
4.下列方程中是一元一次方程的是( )
| A. | x2+5=9 | B. | x+5=x+9 | C. | x+9=2x-10 | D. | $\frac{1}{x}$+5=9 |
3.在平面直角坐标系中,点A(3,4)关于原点的对称点的坐标为( )
| A. | (3,4) | B. | (-3,-4) | C. | (3,-4) | D. | (-3,4) |
20.小强、小亮、小文三位同学玩投硬币游戏.三人同时各投出一枚均匀硬币,若出现三个正面向上或三个反面向上,则小强赢;若出现2个正面向上一个反面向上,则小亮赢;若出现一个正面向上2个反面向上,则小文赢.下面说法正确的是( )
| A. | 三人赢的概率都相等 | B. | 小文赢的概率最小 | ||
| C. | 小亮赢的概率最小 | D. | 小强赢的概率最小 |
 如图,与∠2互为同旁内角的是∠1,∠3;与∠3互为同位角的是∠4,∠5;∠6与∠9是内错角,它们是直线AC与DE被直线BE所截得的;∠3与∠5是直线AC与直线BC被直线BE所截得的;与∠1是同位角的有∠7,∠8,在标有数字的九个角中,大小一定相等的角有∠2=∠6,∠5=∠7.
如图,与∠2互为同旁内角的是∠1,∠3;与∠3互为同位角的是∠4,∠5;∠6与∠9是内错角,它们是直线AC与DE被直线BE所截得的;∠3与∠5是直线AC与直线BC被直线BE所截得的;与∠1是同位角的有∠7,∠8,在标有数字的九个角中,大小一定相等的角有∠2=∠6,∠5=∠7.