题目内容
20.小强、小亮、小文三位同学玩投硬币游戏.三人同时各投出一枚均匀硬币,若出现三个正面向上或三个反面向上,则小强赢;若出现2个正面向上一个反面向上,则小亮赢;若出现一个正面向上2个反面向上,则小文赢.下面说法正确的是( )| A. | 三人赢的概率都相等 | B. | 小文赢的概率最小 | ||
| C. | 小亮赢的概率最小 | D. | 小强赢的概率最小 |
分析 用树状图法表示出所求情况,利用概率公式求得每个人获胜的概率,即可作出判断.
解答 解:列树状图:
则P(三个正面或三个反面向上)=$\frac{2}{8}$=$\frac{1}{4}$,即小强获胜的概率是$\frac{1}{4}$;
P(出现2个正面向上一个反面向上)=$\frac{3}{8}$,即小亮获胜的概率是$\frac{3}{8}$;
P(出现一个正面和2个反面向上)=$\frac{3}{8}$,即小文获胜的概率是$\frac{3}{8}$.
则小强获胜的概率最小,小亮和小文获胜的概率相等.
故正确的答案只有D.
故选D.
点评 本题主要考查了事件的分类和概率的求法.用到的知识点为:可能发生,也可能不发生的事件叫做随机事件;概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
11. 如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
 如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )| A. | ($\frac{2}{3}$,3),(-$\frac{1}{2}$,4) | B. | ($\frac{7}{4}$,$\frac{7}{2}$),($-\frac{1}{2}$,4) | C. | ($\frac{2}{3}$,3),($-\frac{2}{3}$,4) | D. | ($\frac{7}{4}$,$\frac{7}{2}$),($-\frac{2}{3}$,4) |
12.解方程$\frac{3x+1}{2}$-$\frac{10x+1}{6}$=2时,去分母、去括号后,正确结果是( )
| A. | 9x+1-10x+1=1 | B. | 9x+3-10x-1=1 | C. | 9x+3-10x-1=12 | D. | 9x+3-10x+1=12 |
16.多项式49a3bc3+14a2b2c2在分解因式时应提取的公因式是( )
| A. | 7a3bc3 | B. | 7a2b2c2 | C. | 7ab2c2 | D. | 7a2bc2 |
8.下列函数:①y=-x,②y=2x+1,③y=x2+x-1,④y=$\frac{1}{x+2}$其中一次函数为( )
| A. | ①②③④ | B. | ①②④ | C. | ②④ | D. | ①② |
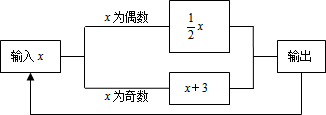 有一个程序机(如图),若输入4,则输出值是2,记作第一次操作;将2再次输入,则输出值是1,记作第二次操作…,则第2016次操作输出的数是4.
有一个程序机(如图),若输入4,则输出值是2,记作第一次操作;将2再次输入,则输出值是1,记作第二次操作…,则第2016次操作输出的数是4. 已知抛物线y=ax2+x+c(a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C,该抛物线的顶点为点M,对称轴与直线BC相交于点N,与x轴相交于点D.
已知抛物线y=ax2+x+c(a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C,该抛物线的顶点为点M,对称轴与直线BC相交于点N,与x轴相交于点D.