题目内容
9.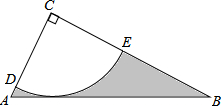 如图,Rt△ABC中,∠C=90°,AC=$\sqrt{5}$,tanB=$\frac{1}{2}$,半径为2的⊙C,分别交AC,BC于点D,E,得到$\widehat{DE}$.
如图,Rt△ABC中,∠C=90°,AC=$\sqrt{5}$,tanB=$\frac{1}{2}$,半径为2的⊙C,分别交AC,BC于点D,E,得到$\widehat{DE}$.(1)求证:AB为⊙C的切线;
(2)求图中阴影部分的面积.
分析 (1)过点C作CH⊥AB于H,如图,先在Rt△ABC中,利用正切的定义计算出BC=2AC=2$\sqrt{5}$,再利用勾股定理计算出AB=5,接着利用面积法计算出CH=2,则可判断CH为⊙C的半径,然后根据切线的判定定理即可得到AB为⊙C的切线;
(2)根据三角形面积公式和扇形的面积公式,利用S阴影部分=S△ACB-S扇形CDE进行计算即可.
解答 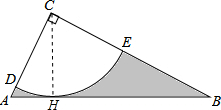 (1)证明:过点C作CH⊥AB于H,如图,
(1)证明:过点C作CH⊥AB于H,如图,
在Rt△ABC中,∵tanB=$\frac{AC}{BC}$=$\frac{1}{2}$,
∴BC=2AC=2$\sqrt{5}$,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{(\sqrt{5})^{2}+(2\sqrt{5})^{2}}$=5,
∵$\frac{1}{2}$CH•AB=$\frac{1}{2}$AC•BC,
∴CH=$\frac{\sqrt{5}×2\sqrt{5}}{5}$=2,
∵⊙C的半径为2,
∴CH为⊙C的半径,
而CH⊥AB,
∴AB为⊙C的切线;
(2)解:S阴影部分=S△ACB-S扇形CDE
=$\frac{1}{2}$×2×5-$\frac{90•π•{2}^{2}}{360}$
=5-π.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径.也考查了勾股定理和扇形面积的计算.

练习册系列答案
相关题目
4.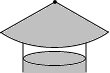 如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )
如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )
 如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )
如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )| A. | 288° | B. | 144° | C. | 216° | D. | 120° |
1.计算(a2)3的结果为( )
| A. | a4 | B. | a5 | C. | a6 | D. | a9 |
18.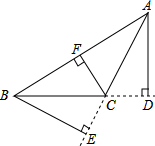 如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D、点E、点F,△ABC中AC边上的高是( )
如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D、点E、点F,△ABC中AC边上的高是( )
 如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D、点E、点F,△ABC中AC边上的高是( )
如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D、点E、点F,△ABC中AC边上的高是( )| A. | CF | B. | BE | C. | AD | D. | CD |
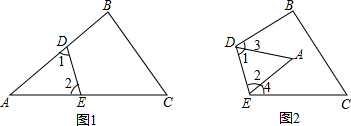
 如图,在六边形ABCDEF中,AF∥CD,AB∥DE,BC∥EF,且∠A=110°,∠B=82°,试求六边形其余各角的度数.
如图,在六边形ABCDEF中,AF∥CD,AB∥DE,BC∥EF,且∠A=110°,∠B=82°,试求六边形其余各角的度数.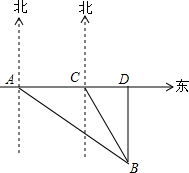 如图,新城区新建了三个商业城A,B,C,其中C在A的正东方向,在A处测得B在A的南偏东52°的方向,在C处测得B在C的南偏东26°的方向,已知A和B的距离是1000m.现有甲、乙两个工程对修建道路,甲修建一条从A到C的笔直道路AC,乙修建一条从B到直线AC最近的道路BD.求甲、乙修建的道路各是多长.(结果精确到1m)(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
如图,新城区新建了三个商业城A,B,C,其中C在A的正东方向,在A处测得B在A的南偏东52°的方向,在C处测得B在C的南偏东26°的方向,已知A和B的距离是1000m.现有甲、乙两个工程对修建道路,甲修建一条从A到C的笔直道路AC,乙修建一条从B到直线AC最近的道路BD.求甲、乙修建的道路各是多长.(结果精确到1m)(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,sin64°≈0.90,cos64°≈0.44,tan64°≈2.05) 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论: