题目内容
5.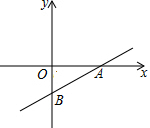 如图,直线AB分别与x轴、y轴交于A、B两点,直线AB与x轴的夹角为30°,且点B(0,-2),求直线AB的函数关系式.
如图,直线AB分别与x轴、y轴交于A、B两点,直线AB与x轴的夹角为30°,且点B(0,-2),求直线AB的函数关系式.
分析 解直角三角形求出OA,得出A点的坐标,直线AB的解析式为y=kx+b,把A、B的坐标代入即可求出k、b,即可得出答案.
解答 解:∵点B(0,-2),
∴OB=2,
∵∠BOA=90°,
∴AB=2OB=4,OA=$\sqrt{3}$OB=2$\sqrt{3}$,
即A的坐标为(2$\sqrt{3}$,0),
设直线AB的解析式为y=kx+b,
把A、B的坐标代入得:$\left\{\begin{array}{l}{b=-2}\\{2\sqrt{3}k+b=0}\end{array}\right.$,
解得:k=$\frac{\sqrt{3}}{3}$,b=-2,
所以直线AB的函数关系式为y=$\frac{\sqrt{3}}{3}$x-2.
点评 本题考查了解直角三角形,用待定系数法求一次函数的解析式的应用,会用待定系数法求函数解析式是解此题的关键.

练习册系列答案
相关题目
15.若点(x1,y1)、(x2,y2)、(x3,y3)都是反比例函数y=$\frac{\sqrt{3}-2}{x}$图象上的点,且且x1<x2<0<x3,则下列正确的是( )
| A. | y1>y2>y3 | B. | y2>y3>y1 | C. | y2>y1>y3 | D. | y1>y3>y2 |
16.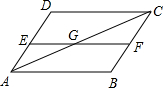 如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,则图中与∠AGE相等的角( )
如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,则图中与∠AGE相等的角( )
 如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,则图中与∠AGE相等的角( )
如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,则图中与∠AGE相等的角( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
14.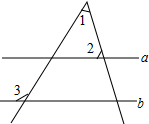 如图,直线a∥b,若∠1=40°,∠2=55°,则∠3等于( )
如图,直线a∥b,若∠1=40°,∠2=55°,则∠3等于( )
 如图,直线a∥b,若∠1=40°,∠2=55°,则∠3等于( )
如图,直线a∥b,若∠1=40°,∠2=55°,则∠3等于( )| A. | 85° | B. | 95° | C. | 105° | D. | 115° |

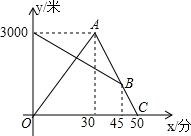 某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,则下列说法:
某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,则下列说法: 如图,在边长为1个单位长度的小正方形网格中.
如图,在边长为1个单位长度的小正方形网格中.