题目内容
已知a、b满足
+|b-
|=0,解关于x的方程(a+3)x+b2=a+6.
| 2a+10 |
| 5 |
考点:非负数的性质:算术平方根,非负数的性质:绝对值
专题:
分析:根据非负数的性质列式求出a、b的值,然后代入代数式得到关于x的一元一次方程,求解即可.
解答:
解:由题意得:2a+10=0,且b-
=0,
解得:a=-5,b=
,
将a=-5,b=
代入原方程,
得:-2x=-4,
解得:x=2.
| 5 |
解得:a=-5,b=
| 5 |
将a=-5,b=
| 5 |
得:-2x=-4,
解得:x=2.
点评:本题考查了绝对值非负数,算术平方根非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0列式是解题的关键.

练习册系列答案
相关题目
下列运算正确的是( )
| A、a2+a4=a6 |
| B、2a×4a=8a |
| C、(a2)3=a6 |
| D、a6÷a3=a2 |
使得函数y=
的函数值为负数的自变量x的取值范围是( )
| 3 |
| 2x+1 |
A、x>-
| ||
B、x<-
| ||
C、x>
| ||
D、x<
|
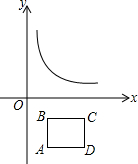 如图,矩形ABCD的边AB=2,BC=4,且BC∥x轴,已知点A的坐标是(2,4).
如图,矩形ABCD的边AB=2,BC=4,且BC∥x轴,已知点A的坐标是(2,4). 如图,△ABC≌△EBD,点C在BE上,若CE=2,BD=3,则AB的长度是
如图,△ABC≌△EBD,点C在BE上,若CE=2,BD=3,则AB的长度是
 如图.在△ABC中,∠A=2∠B,外角∠ACD=150°,求∠B度数.
如图.在△ABC中,∠A=2∠B,外角∠ACD=150°,求∠B度数.