题目内容
4.如果a与b互为倒数,c与d互为相反数,|m|=3,求代数式ab-c-d+$\frac{m}{3}$的值.分析 首先根据a与b互为倒数,可得ab=1;然后根据c与d互为相反数,可得c+d=0,再根据|m|=3,可得m=±3;最后代入原式即可.
解答 解:∵a与b互为倒数,
∴ab=1;
∵c与d互为相反数,
∴c+d=0;
∵|m|=3,
∴m=±3,
(1)当m=3时,
原式=ab-(c+d)+$\frac{m}{3}$=1-0+1=2;
(2)当x=-3时,
原式=ab-(c+d)+$\frac{m}{3}$=1-0-1=0;
综上所述,ab-c-d+$\frac{m}{3}$的值是2或0.
点评 此题主要考查了代数式求值问题,采用代入法即可,解答此题的关键是掌握倒数、相反数及绝对值得定义.

练习册系列答案
相关题目
19.已知函数y=x2+3x+c向右平移3个单位后过原点,那么c的值为( )
| A. | 0 | B. | -18 | C. | 3 | D. | -3 |
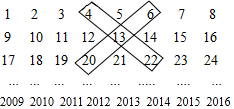
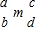 表示类似“X”形框中的5个数,试用等式写出a、b、c、d、m这五个字母之间的关系a+b+c+d=4m(写出一个即可).
表示类似“X”形框中的5个数,试用等式写出a、b、c、d、m这五个字母之间的关系a+b+c+d=4m(写出一个即可).