题目内容
两个反比例函数y=| k |
| x |
| 1 |
| x |
| k |
| x |
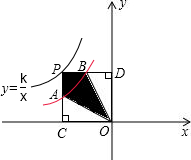 轴于点C交y=-
轴于点C交y=-| 1 |
| x |
| 1 |
| x |
| k |
| x |
①-1<k<0; ②k<-1;
③△ODB与△OAC的面积相等;
④四边形PAOB的面积不会发生变化;
⑤PA与PB始终相等;
⑥当点B是PD的中点时,点A一定是PC的中点.
其中一定正确的是
分析:根据反比例函数的图象的性质,特别是根据反比例函数k的几何意义,对各小题逐一进行分析,即可得出正确答案.
解答:解:根据题意,点P与点A的横坐标相同,都是负数,点P的纵坐标大于点A的纵坐标,
∴
>-
,
解得k<-1,
∴①错误,②正确;
∵y=-
,
∴S△ODB=
×|x|•|y|=
,
S△OCA=
×|x|•|y|=
,
∴S△ODB=S△OCA,故③正确.
∵点P在y=
上,
∴S矩形PCOD=|x|•|y|=|k|,
∴S四边形PAOB=S矩形PCOD-S△ODB-S△OCA=|k|-
-
=-k-1,
∴四边形PAOB的面积不会发生变化,故④正确;
设点P的坐标是(a,
),则点A的坐标是(a,-
),
则PA=
-(-
)=
+
,
∵点B的纵坐标为
,
∴-
=
,
解得x=-
,
∴点B的横坐标是-
,
∴PB=-
-a,
若PA=PB,则
+
=-
-a,
整理得
=-a,
∴当且仅当点P的横坐标与纵坐标的长度相等时,
即四边形PCOD是正方形是,PA=PB,故⑤错误;
∵点B是PD的中点,
∴a=2(-
),
∴k=-2,
又点P的纵坐标是
,即-
,点A的坐标是-
,
∴-
=2(-
),
∴点A一定是PC的中点,故⑥正确.
综上所述,一定正确的是②③④⑥.
故答案为:②③④⑥.
∴
| k |
| x |
| 1 |
| x |
解得k<-1,
∴①错误,②正确;
∵y=-
| 1 |
| x |
∴S△ODB=
| 1 |
| 2 |
| 1 |
| 2 |
S△OCA=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ODB=S△OCA,故③正确.
∵点P在y=
| k |
| x |
∴S矩形PCOD=|x|•|y|=|k|,
∴S四边形PAOB=S矩形PCOD-S△ODB-S△OCA=|k|-
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形PAOB的面积不会发生变化,故④正确;
设点P的坐标是(a,
| k |
| a |
| 1 |
| a |
则PA=
| k |
| a |
| 1 |
| a |
| k |
| a |
| 1 |
| a |
∵点B的纵坐标为
| k |
| a |
∴-
| 1 |
| x |
| k |
| a |
解得x=-
| a |
| k |
∴点B的横坐标是-
| a |
| k |
∴PB=-
| a |
| k |
若PA=PB,则
| k |
| a |
| 1 |
| a |
| a |
| k |
整理得
| k |
| a |
∴当且仅当点P的横坐标与纵坐标的长度相等时,
即四边形PCOD是正方形是,PA=PB,故⑤错误;
∵点B是PD的中点,
∴a=2(-
| a |
| k |
∴k=-2,
又点P的纵坐标是
| k |
| a |
| 2 |
| a |
| 1 |
| a |
∴-
| 2 |
| a |
| 1 |
| a |
∴点A一定是PC的中点,故⑥正确.
综上所述,一定正确的是②③④⑥.
故答案为:②③④⑥.
点评:本题考查反比例函数的综合运用,综合性较强,关键是知道函数图象上的点和坐标轴构成的三角形的面积和四边形的面积和k的关系.

练习册系列答案
相关题目
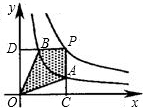 ,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,下列说法正确的是( )
,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,下列说法正确的是( ) 如图,两个反比例函数
如图,两个反比例函数
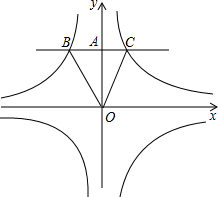 如图,已知反比例函数y=
如图,已知反比例函数y= 已知两个反比例函数
已知两个反比例函数