题目内容
5.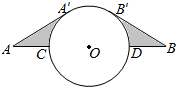 如图,A、B两点之间的距离为4,以AB的中点O为圆心作圆,与线段AB交于C、D两点,已知⊙O的半径为1,AA′,BB′分别与⊙O相切于点A′,B′,则图阴影部分的面积是$\sqrt{3}-\frac{π}{3}$.
如图,A、B两点之间的距离为4,以AB的中点O为圆心作圆,与线段AB交于C、D两点,已知⊙O的半径为1,AA′,BB′分别与⊙O相切于点A′,B′,则图阴影部分的面积是$\sqrt{3}-\frac{π}{3}$.
分析 连接OA′,OB′,根据切线的性质得到∠A′=∠B′=90°,由直角三角形的性质得到∠A=∠B=30°,根据三角形内角和得到∠AOA′=∠BOB′=60°,根据勾股定理得到AA′=BB′=$\sqrt{A{O}^{2}-OA{′}^{2}}$=$\sqrt{3}$,即可得到结论.
解答  解:连接OA′,OB′,
解:连接OA′,OB′,
∵AA′,BB′分别与⊙O相切于点A′,B′,
∴∠A′=∠B′=90°,
∵AB=4,O是AB的中点,
∴AO=OB=2,
∵OA′=OB′=1,
∴∠A=∠B=30°,
∴∠AOA′=∠BOB′=60°,
∴AA′=BB′=$\sqrt{A{O}^{2}-OA{′}^{2}}$=$\sqrt{3}$,
∴阴影部分的面积=2×($\frac{1}{2}×1×\sqrt{3}-\frac{60•π•{1}^{2}}{360}$)=$\sqrt{3}-\frac{π}{3}$.
故答案为:$\sqrt{3}-\frac{π}{3}$.
点评 本题主要考查了扇形面积的求法,切线的性质,在解题时要注意面积计算公式和图形的有关性质的综合应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.下列说法中不正确的是( )
| A. | 直线AB和直线BA是同一条直线 | |
| B. | 平面上两点间的线段的长度叫做这两点的距离 | |
| C. | 四条直线相交最多有六个交点 | |
| D. | 平面上如果AB=BC,则B点是线段AC的中点 |
20. 把两块三角板按如图所示拼在一起,∠BOC=58°,则∠AOD的大小是( )
把两块三角板按如图所示拼在一起,∠BOC=58°,则∠AOD的大小是( )
 把两块三角板按如图所示拼在一起,∠BOC=58°,则∠AOD的大小是( )
把两块三角板按如图所示拼在一起,∠BOC=58°,则∠AOD的大小是( )| A. | 90° | B. | 100° | C. | 120° | D. | 122° |
17.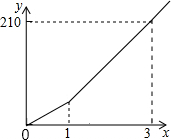 一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图4所示,已知开始1小时的行驶速度是60千米/时,那么1小时以后的速度是( )
一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图4所示,已知开始1小时的行驶速度是60千米/时,那么1小时以后的速度是( )
 一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图4所示,已知开始1小时的行驶速度是60千米/时,那么1小时以后的速度是( )
一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图4所示,已知开始1小时的行驶速度是60千米/时,那么1小时以后的速度是( )| A. | 70千米/时 | B. | 75千米/时 | C. | 105千米/时 | D. | 210千米/时 |
15. x、y、z在数轴上的位置如图所示,则化简|x-y|+|z-y|的结果是( )
x、y、z在数轴上的位置如图所示,则化简|x-y|+|z-y|的结果是( )
 x、y、z在数轴上的位置如图所示,则化简|x-y|+|z-y|的结果是( )
x、y、z在数轴上的位置如图所示,则化简|x-y|+|z-y|的结果是( )| A. | x+z-2y | B. | 2y-x-z | C. | z-x | D. | x-z |
 已知,如图,CD为⊙O的直径,∠EOD=60°,AE交⊙O于点B,E,且AB=OC,求:∠A的度数.
已知,如图,CD为⊙O的直径,∠EOD=60°,AE交⊙O于点B,E,且AB=OC,求:∠A的度数. 如图,在边长为100米的正三角形花坛的边上,甲、乙两人分别从两个顶点同时出发,按逆时针方向行走,已知甲的速度是42米/分,乙的速度是34米/分.出发后$\frac{100}{7}$分钟,甲乙两人第一次走在同一条边上.
如图,在边长为100米的正三角形花坛的边上,甲、乙两人分别从两个顶点同时出发,按逆时针方向行走,已知甲的速度是42米/分,乙的速度是34米/分.出发后$\frac{100}{7}$分钟,甲乙两人第一次走在同一条边上.