题目内容
10. 如图,在边长为100米的正三角形花坛的边上,甲、乙两人分别从两个顶点同时出发,按逆时针方向行走,已知甲的速度是42米/分,乙的速度是34米/分.出发后$\frac{100}{7}$分钟,甲乙两人第一次走在同一条边上.
如图,在边长为100米的正三角形花坛的边上,甲、乙两人分别从两个顶点同时出发,按逆时针方向行走,已知甲的速度是42米/分,乙的速度是34米/分.出发后$\frac{100}{7}$分钟,甲乙两人第一次走在同一条边上.
分析 计算出乙在AB、BC、CA、AB、BC上所用的时间,再计算出甲行走的距离,判断甲乙两人是否第一次走在同一条边上.
解答  解:①乙在AB上时,时间范围为0≤t≤$\frac{50}{17}$分,甲走的路程为0米≤t≤$\frac{2100}{17}$米,甲在BC或AC上;
解:①乙在AB上时,时间范围为0≤t≤$\frac{50}{17}$分,甲走的路程为0米≤t≤$\frac{2100}{17}$米,甲在BC或AC上;
②乙在BC上时,时间范围为$\frac{50}{17}$≤t≤$\frac{100}{17}$分,甲走的路程为米$\frac{2100}{17}$≤t≤$\frac{4200}{17}$米,甲在AB或AC上;
③乙在CA上时,时间范围为$\frac{100}{17}$≤t≤$\frac{150}{17}$分,甲走的路程为米$\frac{4200}{17}$≤t≤$\frac{6300}{17}$米,甲在AB或BC上;
④乙又到AB上时,时间范围为$\frac{150}{17}$≤t≤$\frac{200}{17}$分,甲走的路程为米$\frac{6300}{17}$≤t≤$\frac{8400}{17}$米,甲在AC或BC上;
⑤乙又到BC上时,时间范围为$\frac{200}{17}$≤t≤$\frac{250}{17}$分,甲走的路程为米$\frac{8400}{17}$≤t≤$\frac{10500}{17}$米,甲在AC或BC上.
当甲走过600米时,刚好在点B,这时候乙走过大约486米,在BC边上,这时候恰好在BC边上.
t=$\frac{600}{42}$=$\frac{100}{7}$分钟.
点评 本题考查的是等边三角形的性质,熟知等边三角形的三边相等是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.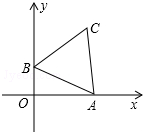 如图,边长为2的等边△ABC的顶点A,B分别在x轴正半轴和y轴正半轴上运动,则动点C到原点O的距离的最大值是( )
如图,边长为2的等边△ABC的顶点A,B分别在x轴正半轴和y轴正半轴上运动,则动点C到原点O的距离的最大值是( )
 如图,边长为2的等边△ABC的顶点A,B分别在x轴正半轴和y轴正半轴上运动,则动点C到原点O的距离的最大值是( )
如图,边长为2的等边△ABC的顶点A,B分别在x轴正半轴和y轴正半轴上运动,则动点C到原点O的距离的最大值是( )| A. | $\sqrt{3}-1$ | B. | $\sqrt{3}+1$ | C. | $\sqrt{6}-1$ | D. | $\sqrt{6}+1$ |
15.如果|-a|=a,则下列a的取值不能使这个式子成立的是( )
| A. | 0 | B. | 1 | C. | 2 | D. | a取任何负数 |
19.下列各组式子中,同类项是( )
| A. | 2a2b与3ab2 | B. | -x2y与4yx2 | C. | ax2与bx2 | D. | 3a2与4a3 |
 如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.
如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.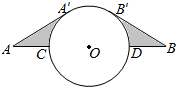 如图,A、B两点之间的距离为4,以AB的中点O为圆心作圆,与线段AB交于C、D两点,已知⊙O的半径为1,AA′,BB′分别与⊙O相切于点A′,B′,则图阴影部分的面积是$\sqrt{3}-\frac{π}{3}$.
如图,A、B两点之间的距离为4,以AB的中点O为圆心作圆,与线段AB交于C、D两点,已知⊙O的半径为1,AA′,BB′分别与⊙O相切于点A′,B′,则图阴影部分的面积是$\sqrt{3}-\frac{π}{3}$.