题目内容
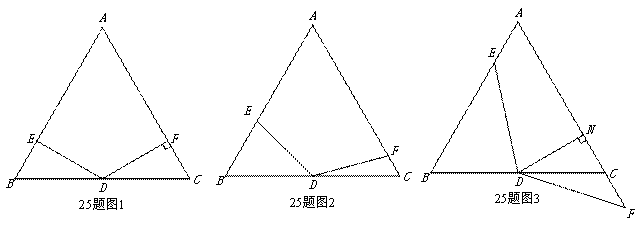
在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF扔与线段AC相交于点F.求证: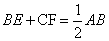 ;
;
(3)如图3,将(2)中的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线交与点F,作DN⊥AC于点N,若DN=FN,求证: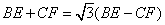 .
.
13. 解:
⑴由四边形AEDF的内角和为 ,可知DE⊥AB,故
,可知DE⊥AB,故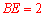
⑵取AB的中点G,连接DG
易证:DG为△ABC的中位线,故DG=DC,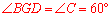
又四边形AEDF的对角互补,故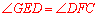
∴△DEG≌△DFC
故EG=CF
∴BE+CF=BE+EG=BG=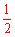 AB
AB
⑶取AB的中点G,连接DG
同⑵,易证△DEG≌△DFC
故EG=CF
故BE-CF=BE-EG=BG=
设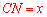
在Rt△DCN中,CD=2x,DN=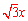
在RT△DFN中,NF=DN=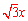 ,故EG=CF=
,故EG=CF=
BE=BG+EG=DC+CF=2x+ =
=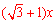
故BE+CF=
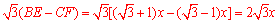
故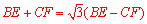

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
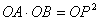 ,我们就把∠APB叫做∠MON的智慧角.
,我们就把∠APB叫做∠MON的智慧角.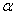 (0°<
(0°<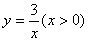 图象上的一个动点,过点C的直线CD分别交
图象上的一个动点,过点C的直线CD分别交 轴和
轴和 轴于点A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
轴于点A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.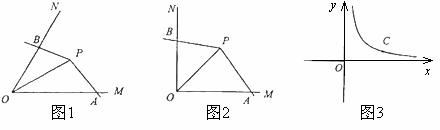
 、
、 、
、 ,求这个三角形的面积.
,求这个三角形的面积.
 、
、 、
、 ,请利用图2的正方形网格(每个小正方形的边长为
,请利用图2的正方形网格(每个小正方形的边长为 )画出相应的△ABC,并求出它的面积是: .
)画出相应的△ABC,并求出它的面积是: . 、
、 、
、
 ,请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为: .
,请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为: . ;
; 中,自变量
中,自变量 的取值范围是( )
的取值范围是( )
 B.
B. C.
C. D.
D.
 定规律组成,其中第①个图形含边长为1的菱形3个,第②个图形含边长为1的菱形6个,第③个图形含边长为1的菱形10个,... ...,按此规律,则第⑦个图形中含边长为1的菱形的个数为( )
定规律组成,其中第①个图形含边长为1的菱形3个,第②个图形含边长为1的菱形6个,第③个图形含边长为1的菱形10个,... ...,按此规律,则第⑦个图形中含边长为1的菱形的个数为( )
 (B)
(B) (C)
(C) (D)
(D)
 >1-
>1- .
.