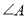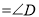��Ŀ����
��ͼ��ƽ��ֱ������ϵ�У�OΪ����ABCD�ĶԳ����ģ���֪C��2��0����D��0����1����NΪ�߶�CD��һ�㣨����C��D�غϣ���
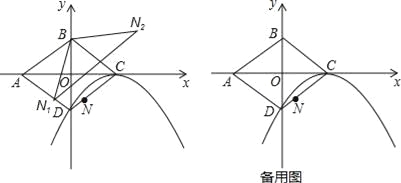
��1������CΪ���㣬�Ҿ�����D�������߽���ʽ��
��2����N����BD�ĶԳƵ�ΪN1��N����BC�ĶԳƵ�ΪN2����֤����N1BN2�ס�ABC��
��3����2����N1N2����Сֵ��
��4������N��y���ƽ���߽���1���е��������ڵ�P����QΪֱ��AB�ϵ�һ�����㣬�ҡ�PQA=��BAC����PQ��Сʱ��Q���꣮
��1��y=����x��2��2��2��֤����������3����4�� �������������������1���ô���ϵ�������ɣ� ��2���ɶԳƵ��ص�ó���N1BN2=2��DBC������ε����ʼ��ɣ� ��3�����ж�������BN��CDʱ��BN��̣������á�ABC�ס�N1BN2�õ�����ʽ����⣬���ɣ� ��4���Ƚ���PE=m2��m+2��������ʽ�����������ߵ��ص�ȷ������Сֵ�� �����������1������֪��������...
��ϰ��ϵ�д�
 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
�����Ŀ



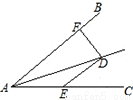
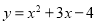 ��
��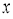 �����������Ϊ
�����������Ϊ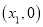 ��
��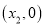 ��
��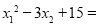 ��
��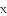
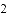
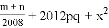 ��ֵ.
��ֵ.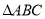 ��
��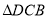 �������ǣ�������
�������ǣ�������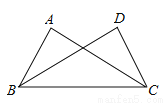
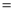 DC��AC
DC��AC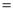 DB B. AB
DB B. AB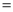 DC��
DC�� 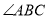
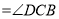
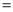 DC��
DC�� 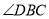
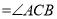 D.
D. 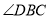
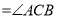 ��
��