题目内容
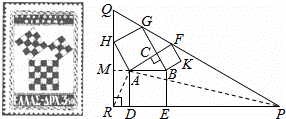
勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发型了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQO使得∠O=90°,点Q在在直角坐标系y轴正半轴上,点P在x轴正半轴上,点O与原点重合,∠OQP=60°,点H在边QO上,点D、E在边PO上,点G、F在边PQ上,那么点P坐标为 .
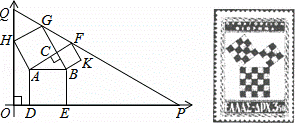
(7 +6,0) 解:延长BA交QR于点M,连接AR,AP,
+6,0) 解:延长BA交QR于点M,连接AR,AP,
在△ABC与△GFC中,
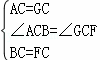 ,
,
∴△ABC≌△GFC(SAS),
∴∠CGF=∠BAC=30°,
∴∠HGQ=60°,
∵∠HAC=∠BAD=90°,
∴∠BAC+∠DAH=180°,
又∵AD∥QR,
∴∠RHA+∠DAH=180°,
∴∠RHA=∠BAC=30°,
∴∠QHG=60°,
∴∠Q=∠QHG=∠QGH=60°,
∴△QHG是等边三角形.
AC=AB•cos30°=4×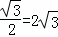 ,
,
则QH=HA=HG=AC=2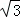 ,
,
在直角△HMA中,HM=AH•sin60°=2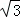 ×
× =3.AM=HA•cos60°=
=3.AM=HA•cos60°=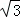 ,
,
在直角△AMR中,MR=AD=AB=4,
∴QR=2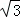 +3+4=7+2
+3+4=7+2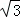 ,
,
∴QP=2QR=14+4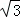 ,
,
PR=QR•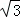 =7
=7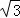 +6,
+6,
∴点P的坐标为(7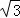 +6,0).
+6,0).
故答案为:(7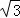 +6,0).
+6,0).

练习册系列答案
相关题目
 ﹣
﹣ +
+ ;
; 整数解共有2个,则m的取值范围是( )
整数解共有2个,则m的取值范围是( )
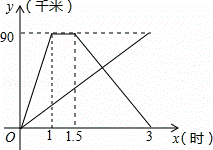
 )求甲从B地返回A地的过程中,y与x之间的函数关系式,并写出自变量x的取值范围;
)求甲从B地返回A地的过程中,y与x之间的函数关系式,并写出自变量x的取值范围;