��Ŀ����
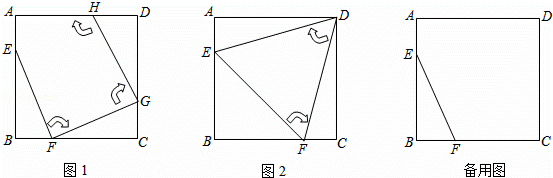
��ͼ1���߳�Ϊ4��������ABCD�У���E��AB���ϣ������A��B�غϣ�����F��BC���ϣ������B��C�غϣ���
��һ�β��������߶�EF�Ƶ�F˳ʱ����ת������E������������ʱ����Ϊ��G��
�ڶ��β��������߶�FG�Ƶ�G˳ʱ����ת������F������������ʱ����Ϊ��H��
���β�����ȥ��
��1��ͼ2�еġ�EFD�Ǿ������β�����õ��ģ�����״Ϊ�� �������ʱ�߶�EF�ij���
��2�����������β����ɵõ��ı���EFGH��
�����ж��ı���EFGH����״Ϊ�� ������ʱAE��BF��������ϵ���� ����
���Ԣ��еĽ���Ϊǰ�ᣬ��AE�ij�Ϊx���ı���EFGH�����Ϊy����y��x�ĺ�����ϵʽ�����y��ȡֵ��Χ��
��3����������β����ɵõ���β˳����ӵĶ���Σ����������Ƕ��٣����������������������ǣ���ֱ��д����߳���������ǣ���˵�����ɣ�
�⣺��1������ͼ2������ת���ʿ�֪EF=DF=DE�����DEFΪ�ȱ������Σ�
��Rt��ADE��Rt��CDF��

��Rt��ADE��Rt��CDF��HL��
��AE=CF��
��AE=CF=x����BE=BF=4﹣x
���BEFΪ����ֱ�������Σ�
��EF=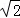 BF=
BF=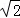 ��4﹣x����
��4﹣x����
��DE=DF=EF=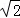 ��4﹣x����
��4﹣x����
��Rt��ADE�У��ɹ��ɶ����ã�AE2+AD2=DE2������x+42=[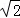 ��4﹣x]2��
��4﹣x]2��
��ã�x1=8﹣4 ��x2=8+4
��x2=8+4 ����ȥ��
����ȥ��
��EF=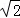 ��4﹣x��=4
��4﹣x��=4 ﹣4
﹣4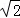 ��
��
DEF����״Ϊ�ȱ������Σ�EF�ij�Ϊ4 ﹣4
﹣4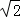 ��
��
��2�����ı���EFGH����״Ϊ�����Σ���ʱAE=BF���������£�
�����⻭��ͼ�Σ����ͼ1��ʾ��

����ת���ʿ�֪��EF=FG=GH=HE�����ı���EFGH����״Ϊ�����Σ�
�ߡ�1+��2=90�㣬��2+��3=90�㣬
���1=��3��
�ߡ�3+��4=90�㣬��2+��3=90�㣬
���2=��4��
�ڡ� AEH���BFE�У�
AEH���BFE��

���AEH�ա�BFE��ASA��
��AE=BF��
�����â��н��ۣ���֤��AEH����BFE����CGF����DHG��Ϊȫ�������Σ�
��BF=CG=DH=AE=x��AH=BE=CF=DG=4﹣x��
��y=S������ABCD﹣4S��AEH=4��4﹣4��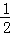 x��4﹣x��=2x2﹣8x+16��
x��4﹣x��=2x2﹣8x+16��
��y=2x2﹣8x+16��0��x��4��
��y=2x2﹣8x+16=2��x﹣2��2+8��
�൱x=2ʱ��yȡ����Сֵ8����x=0ʱ��y=16��
��y��ȡֵ��ΧΪ��8��y��16��
��3��������β����ɵõ���β˳����ӵĶ���Σ�����������8��������Ϊ������Σ��߳�Ϊ4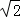 ﹣4��
﹣4��
���ͼ2��ʾ�����߲��������߶�EF����7�β������γɵ����˱��Σ�
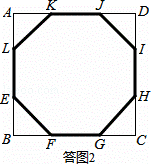
��߳�EF=FG=x����BF=CG= x��
x��
BC=BF+FG+CG= x+x+
x+x+ x=4����ã�x=4
x=4����ã�x=4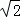 ﹣4��
﹣4��

 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д����м������У�����ͼ�������ε��ǣ�������
| �� | A�� |
| B�� |
| C�� |
| D�� |
|
��֪����������y=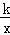 ��ͼ����ͼ������κ���y=2kx2﹣4x+k2��ͼ�����Ϊ��������
��ͼ����ͼ������κ���y=2kx2﹣4x+k2��ͼ�����Ϊ��������
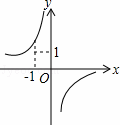
| �� | A�� |
| B�� |
| C�� |
| D�� |
|
��ͼ�м�����ĸ���ͼ�ǣ�������

| �� | A�� |
| B�� |
| C�� |
| D�� |
|












 ����xy��3��ֵΪ��
����xy��3��ֵΪ��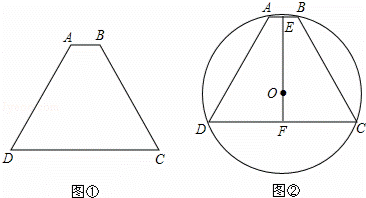
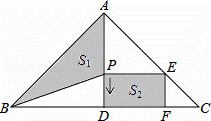
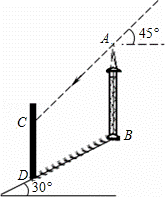
 cm/s���ٶ����D�˶������ABP�����ΪS1������PDFE�����ΪS2���˶�ʱ��Ϊt�루0��t��8������t=
cm/s���ٶ����D�˶������ABP�����ΪS1������PDFE�����ΪS2���˶�ʱ��Ϊt�루0��t��8������t= ������ʱ��S1=2S2��
������ʱ��S1=2S2��