题目内容
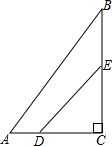 如图,在Rt△ABC中,已知∠ACB=90°,AC=3,BC=4,动点D从点A出发沿射线AC方向以每秒2个单位的速度运动,点E是边BC的中点,连结DE.设点D运动的时间为t秒.求当t取何值时,△ABC与△CDE相似?写出所有的情况.
如图,在Rt△ABC中,已知∠ACB=90°,AC=3,BC=4,动点D从点A出发沿射线AC方向以每秒2个单位的速度运动,点E是边BC的中点,连结DE.设点D运动的时间为t秒.求当t取何值时,△ABC与△CDE相似?写出所有的情况.考点:相似三角形的判定
专题:动点型,分类讨论
分析:分D点在BC的左边和D点在BC的右边两种情况讨论即可求解.
解答:解:∵点E是边BC的中点,
∴CE=
BC=2,
①当D点在BC的左边时,
△CAB与△CDE相似,则
=
,
=
,
解得t=
;
△CAB与△CED相似,则
=
,即
=
,
解得t=
;
②当D点在BC的右边时,
△CAB与△CDE相似,则
=
,即
=
,
解得t=
;
△CAB与△CED相似,则
=
,即
=
,
解得t=
;
故当t取
或
或
或
时,△ABC与△CDE相似.
∴CE=
| 1 |
| 2 |
①当D点在BC的左边时,
△CAB与△CDE相似,则
| CA |
| CD |
| CB |
| CE |
| 3 |
| 3-2t |
| 4 |
| 2 |
解得t=
| 3 |
| 4 |
△CAB与△CED相似,则
| CA |
| CE |
| CB |
| CD |
| 3 |
| 2 |
| 4 |
| 3-2t |
解得t=
| 1 |
| 6 |
②当D点在BC的右边时,
△CAB与△CDE相似,则
| CA |
| CD |
| CB |
| CE |
| 3 |
| 2t-3 |
| 4 |
| 2 |
解得t=
| 9 |
| 4 |
△CAB与△CED相似,则
| CA |
| CE |
| CB |
| CD |
| 3 |
| 2 |
| 4 |
| 2t-3 |
解得t=
| 17 |
| 6 |
故当t取
| 3 |
| 4 |
| 1 |
| 6 |
| 9 |
| 4 |
| 17 |
| 6 |
点评:考查了相似三角形的判定和性质:两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;注意分情况讨论求解.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
下列各数中是无理数的是( )
A、
| |||
B、
| |||
C、
| |||
D、
|
 如图,AD∥BC,若△ABC面积是15,则△DBC的面积是( )
如图,AD∥BC,若△ABC面积是15,则△DBC的面积是( )| A、12 | B、13 | C、14 | D、15 |
方程组
的解是( )
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
 在如图的正方形网格中画出以下三角形(要有答,并把各边的长写在边上)
在如图的正方形网格中画出以下三角形(要有答,并把各边的长写在边上)