题目内容
 如图,等腰直角△ABC中,∠BAC=90°,AB=AC,AD是高,∠ABC的平分线交AD、AC于E、F,点P是BF延长线上一点,且∠APB=45°,连接PC;以下结论:①CF=2DE;②BE=
如图,等腰直角△ABC中,∠BAC=90°,AB=AC,AD是高,∠ABC的平分线交AD、AC于E、F,点P是BF延长线上一点,且∠APB=45°,连接PC;以下结论:①CF=2DE;②BE= PE;③AE•CF=
PE;③AE•CF= AP•EF;④BF•PB+CF•AC=
AP•EF;④BF•PB+CF•AC= AB2.其中正确的结论是
AB2.其中正确的结论是
- A.①②
- B.①③④
- C.①②③
- D.①②③④
C
分析:首先过点F作FG⊥BC于G,由题意易得△ABD,△ACD,△CFG是等腰直角三角形,△AEF与△APE是等腰三角形,然后由△ABF∽△DBE,可求得①正确;再过点P作PH⊥AD于H,由等腰三角形的性质与平行线分线段成比例定理,可求得②正确;又由△ABP∽△FBC,可证得③正确;由△ABP∽△FBC,可得BF•PB=AB•BC= AB2,由CF=
AB2,由CF= FG=
FG= AF,可得CF•AC=(2-
AF,可得CF•AC=(2- )AB2,继而可求得BF•PB+CF•AC=2AB2.
)AB2,继而可求得BF•PB+CF•AC=2AB2.
解答:过点F作FG⊥BC于G,
∵等腰直角△ABC中,∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵AD是高,EF是∠ABC的平分线,
∴∠BAD=∠CAD=45°,∠ABF=∠CBF= ∠ABC=22.5°,FG=FA,
∠ABC=22.5°,FG=FA,
∴△ABD、△ACD与△CFG是等腰直角三角形,
∴AD=BD=CD,
∵∠ABF=∠CBF,∠BAF=∠BDE=90°,
∴△ABF∽△DBE,
∴AF:DE=AB:BD= ,
,
∴AF= DE,
DE,
∴FG= DE,
DE,
∵CF= FG=
FG= ×
× DE=2DE,
DE=2DE,
故①正确;
过点P作PH⊥AD于H,
∵∠APB=45°,∠EAF=45°,∠AEP=∠BED=90°-∠CBF=67.5°,
∴∠PAE=180°-∠APB-∠AEP=67.5°,∠AFE=180°-∠AEF-∠EAF=67.5°,
∴∠PAE=∠AEP,∠EAF=∠AEF,
∴PA=PE,AE=AF,
∴AH=HE,
∴AE=FG= DE,
DE,
∴HE= DE,
DE,
∵∠PHD=∠BDH=90°,
∴PH∥BD,
∴PE:BE=EH:ED= :2,
:2,
∴BE= PE;
PE;
故②正确;
∵∠EAF=∠APB,∠AEF=∠AEP,
∴△AEF∽△PEA,
∴AP:AE=AE:EF,
∴AE2=AP•EF,
∵CF= FG=
FG= AE,
AE,
∴AE•CF= AE2=
AE2= AP•EF;
AP•EF;
故③正确;
∵∠ABP=∠CBP,∠APB=∠ACB=45°,
∴△ABP∽△FBC,
∴AB:BF=PB:BC,
∴AB•BC=BF•PB,
∵BC= AB,
AB,
∴BF•PB=AB•BC= AB2,
AB2,
∵CF= FG=
FG= AF,
AF,
∴CF=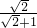 AC=(2-
AC=(2- )AC,
)AC,
∴CF•AC=(2- )AC•AC=(2-
)AC•AC=(2- )AB2,
)AB2,
∴BF•PB+CF•AC= AB2+(2-
AB2+(2- )AB2=2AB2.
)AB2=2AB2.
故④错误.
故选C.
点评:此题考查了相似三角形的判定与性质、等腰三角形的判定与性质以及等腰直角三角形的判定与性质等知识.此题难度较大,注意掌握辅助线的作法,注意数形结合思想与转化思想的应用是解此题的关键.
分析:首先过点F作FG⊥BC于G,由题意易得△ABD,△ACD,△CFG是等腰直角三角形,△AEF与△APE是等腰三角形,然后由△ABF∽△DBE,可求得①正确;再过点P作PH⊥AD于H,由等腰三角形的性质与平行线分线段成比例定理,可求得②正确;又由△ABP∽△FBC,可证得③正确;由△ABP∽△FBC,可得BF•PB=AB•BC=
 AB2,由CF=
AB2,由CF= FG=
FG= AF,可得CF•AC=(2-
AF,可得CF•AC=(2- )AB2,继而可求得BF•PB+CF•AC=2AB2.
)AB2,继而可求得BF•PB+CF•AC=2AB2.解答:过点F作FG⊥BC于G,
∵等腰直角△ABC中,∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵AD是高,EF是∠ABC的平分线,
∴∠BAD=∠CAD=45°,∠ABF=∠CBF=
 ∠ABC=22.5°,FG=FA,
∠ABC=22.5°,FG=FA,∴△ABD、△ACD与△CFG是等腰直角三角形,
∴AD=BD=CD,
∵∠ABF=∠CBF,∠BAF=∠BDE=90°,
∴△ABF∽△DBE,
∴AF:DE=AB:BD=
 ,
,∴AF=
 DE,
DE,∴FG=
 DE,
DE,∵CF=
 FG=
FG= ×
× DE=2DE,
DE=2DE,故①正确;
过点P作PH⊥AD于H,
∵∠APB=45°,∠EAF=45°,∠AEP=∠BED=90°-∠CBF=67.5°,
∴∠PAE=180°-∠APB-∠AEP=67.5°,∠AFE=180°-∠AEF-∠EAF=67.5°,
∴∠PAE=∠AEP,∠EAF=∠AEF,
∴PA=PE,AE=AF,
∴AH=HE,
∴AE=FG=
 DE,
DE,∴HE=
 DE,
DE,∵∠PHD=∠BDH=90°,
∴PH∥BD,
∴PE:BE=EH:ED=
 :2,
:2,∴BE=
 PE;
PE;故②正确;
∵∠EAF=∠APB,∠AEF=∠AEP,
∴△AEF∽△PEA,
∴AP:AE=AE:EF,

∴AE2=AP•EF,
∵CF=
 FG=
FG= AE,
AE,∴AE•CF=
 AE2=
AE2= AP•EF;
AP•EF;故③正确;
∵∠ABP=∠CBP,∠APB=∠ACB=45°,
∴△ABP∽△FBC,
∴AB:BF=PB:BC,
∴AB•BC=BF•PB,
∵BC=
 AB,
AB,∴BF•PB=AB•BC=
 AB2,
AB2,∵CF=
 FG=
FG= AF,
AF,∴CF=
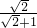 AC=(2-
AC=(2- )AC,
)AC,∴CF•AC=(2-
 )AC•AC=(2-
)AC•AC=(2- )AB2,
)AB2,∴BF•PB+CF•AC=
 AB2+(2-
AB2+(2- )AB2=2AB2.
)AB2=2AB2.故④错误.
故选C.
点评:此题考查了相似三角形的判定与性质、等腰三角形的判定与性质以及等腰直角三角形的判定与性质等知识.此题难度较大,注意掌握辅助线的作法,注意数形结合思想与转化思想的应用是解此题的关键.

练习册系列答案
相关题目
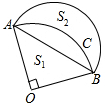 如图,等腰直角三角形AOB的面积为S1,以点O为圆心,OA为半径的弧与以AB为直径的半圆围成的图形的面积为S2,则S1与S2的关系是( )
如图,等腰直角三角形AOB的面积为S1,以点O为圆心,OA为半径的弧与以AB为直径的半圆围成的图形的面积为S2,则S1与S2的关系是( )| A、S1>S2 | B、S1<S2 | C、S1=S2 | D、S1≥S2 |
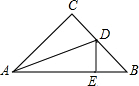 如图,等腰直角三角形ABC中,∠C=90°,AD为∠CAB的平分线,DE⊥AB于E,AC=4,则△BDE的周长为( )
如图,等腰直角三角形ABC中,∠C=90°,AD为∠CAB的平分线,DE⊥AB于E,AC=4,则△BDE的周长为( )| A、4 | ||
| B、6 | ||
C、4
| ||
D、4
|
 (2012•镇江模拟)如图,等腰直角三角形ABC中,AC=BC>3,点M在AC上,点N在CB的延长线上,MN交AB于点O,且AM=BN=3,则S△AMO与S△BNO的差是( )
(2012•镇江模拟)如图,等腰直角三角形ABC中,AC=BC>3,点M在AC上,点N在CB的延长线上,MN交AB于点O,且AM=BN=3,则S△AMO与S△BNO的差是( ) 如图,等腰直角△ABC中,∠ABC=90°,点D在AC上,将△ABD绕顶点B沿顺时针方向旋90°后得到△CBE.
如图,等腰直角△ABC中,∠ABC=90°,点D在AC上,将△ABD绕顶点B沿顺时针方向旋90°后得到△CBE. 如图,等腰直角三角形△ABC中,∠ACB=90°,点D是BC的中点,CE⊥AD于点F交AB于点E,CH是AB上的高交AD于点G.
如图,等腰直角三角形△ABC中,∠ACB=90°,点D是BC的中点,CE⊥AD于点F交AB于点E,CH是AB上的高交AD于点G.