题目内容
12.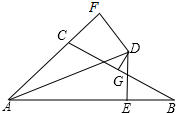 如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,求BE的长.
如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,求BE的长.
分析 首先连接CD,BD,由∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,根据角平分线的性质与线段垂直平分线的性质,易得CD=BD,DF=DE,继而可得AF=AE,易证得Rt△CDF≌Rt△BDE,则可得BE=CF,继而求得答案.
解答 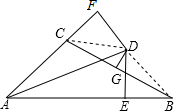 解:如图,连接CD,BD,
解:如图,连接CD,BD,
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DF=DE,∠F=∠DEB=90°,∠ADF=∠ADE,
∴AE=AF,
∵DG是BC的垂直平分线,
∴CD=BD,
在Rt△CDF和Rt△BDE中,
$\left\{\begin{array}{l}{CD=BD}\\{DF=DE}\end{array}\right.$,
∴Rt△CDF≌Rt△BDE(HL),
∴BE=CF,
∴AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE,
∵AB=6,AC=3,
∴BE=1.5.
点评 此题考查了线段垂直平分线的性质、角平分线的性质以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.二次函数y=x2+6x+5的图象与x轴交点的横坐标是( )
| A. | 1和5 | B. | 1和-5 | C. | -1和-5 | D. | -1和5 |
3.某次大型活动由大学生组成仪仗队,若同学甲站在第六行第八列,可以表示为(6,8),则乙同学站第20行第7列,表示为( )
| A. | (7,20) | B. | (20,7) | C. | (7,7) | D. | (20,20) |
7.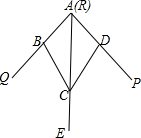 如图,小敏做了一个角平分仪ABCD,其中AB=CD,BC=DC,将仪器上的点与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
如图,小敏做了一个角平分仪ABCD,其中AB=CD,BC=DC,将仪器上的点与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
 如图,小敏做了一个角平分仪ABCD,其中AB=CD,BC=DC,将仪器上的点与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
如图,小敏做了一个角平分仪ABCD,其中AB=CD,BC=DC,将仪器上的点与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )| A. | SSS | B. | ASA | C. | AAS | D. | SAS |
17. 下列四个图形中,属于全等图形的是( )
下列四个图形中,属于全等图形的是( )
 下列四个图形中,属于全等图形的是( )
下列四个图形中,属于全等图形的是( )| A. | ①和② | B. | ②和③ | C. | ①和③ | D. | ②和④ |
2.下列交换加数位置的变形中,正确的是( )
| A. | 1-4+5-4=1-4+4-5 | B. | 1-2+3-4=2-1+4-3 | ||
| C. | 4-7-5+8=4-5+8-7 | D. | -3+4-1-2=2+4-3-1 |
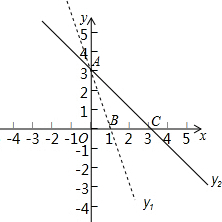 已知函数y1=k1x+b1和y2=k2x+b2图象如图所示,直线y1与直线y2交于A点(0,3).
已知函数y1=k1x+b1和y2=k2x+b2图象如图所示,直线y1与直线y2交于A点(0,3). 2014年12月25日,石家庄至济南客运专线重点控制工程衡景特大桥箱梁架设任务全面展开,该项目在招标时接到了甲、乙两个施工单位的投标书,从投标书中得知如图所示的信息.
2014年12月25日,石家庄至济南客运专线重点控制工程衡景特大桥箱梁架设任务全面展开,该项目在招标时接到了甲、乙两个施工单位的投标书,从投标书中得知如图所示的信息.