题目内容

2．二次函数y=x2+6x+5的图象与x轴交点的横坐标是（　　）
A．1和5B．1和-5C．-1和-5D．-1和5

分析 令y=0得到x2+6x+5=0，然后求得方程的解即可．

解答 解：令y=0得x2+6x+5=0，
解得：x1=-1，x2=-5．
故选：C．

点评 本题主要考查的是抛物线与x轴的交点，将函数问题转化为方程问题是解题的关键．

练习册系列答案
相关题目
12．不能判定四边形ABCD为平行四边形的命题是（　　）
A．AB∥CD且AB=CDB．AB=AD、BC=CDC．AB=CD，AD=BCD．∠A=∠C，∠B=∠D
13．计算或化简
①（-12）-5+（-14）-（-39）
②3$\frac{1}{2}$-（-$\frac{1}{3}$）+2$\frac{2}{3}$+（-$\frac{1}{2}$）
③-14+16÷（-2）3×|-3-1|
④7a2b+（-4a2b+5ab2）-3（a2b-2ab2）
10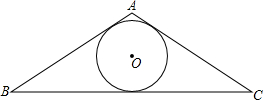．已知：如图，⊙O是△ABC的内切圆，下列说法错误的是（　　）
A．点O在△ABC的三边垂直平分线上
B．点O在△ABC的三个内角平分线上
C．如果△ABC的面积为S，三边长为a，b，c，⊙O的半径为r，那么r=$\frac{2S}{a+b+c}$
D．如果△ABC的三边长分别为5，7，8，那么以A、B、C为端点三条切线长分别为5，3，2
17．将$\sqrt{48}$化为最简二次根式是4$\sqrt{3}$．
7．如图，在△ABC中，AB=AC，∠A=42°，AB的垂直平分线MN交AC于点D．求∠DBC的度数．
14．计算（a3b2）4的结果是（　　）
A．a32b4B．a3b8C．a7b6D．a12b8
11．已知：△ABC．
（1）尺规作图（保留作图痕迹，不写作法）：作AB的垂直平分线MN，使MN交AC于D；
（2）连BD，若AC=3cm，BC=2cm，则△BDC的周长为5cm．
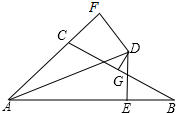12．如图，∠BAC的平分线与BC的垂直平分线相交于点D，DE⊥AB，DF⊥AC，垂足分别为E、F，AB=6，AC=3，求BE的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网