题目内容
20.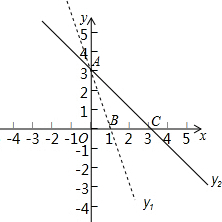 已知函数y1=k1x+b1和y2=k2x+b2图象如图所示,直线y1与直线y2交于A点(0,3).
已知函数y1=k1x+b1和y2=k2x+b2图象如图所示,直线y1与直线y2交于A点(0,3).(1)求函数y1和y2的函数关系式;
(2)求三角形ABC的面积;
(3)已知点D在x轴上,且满足三角形ACD是等腰三角形,直接写出D点坐标.
分析 (1)把点的坐标代入函数解析式即可得到结论;
(2)根据三角形的面积公式计算即可;
(3)根据勾股定理得到AC=3$\sqrt{2}$,①当AD=AC=3$\sqrt{3}$时,根据等腰三角形的性质得到D1(-3,0),②当AC=CD=3$\sqrt{2}$时,根据等腰三角形的性质得到D2(3-3$\sqrt{2}$,0),③当AD=PD=3时,D在AC的垂直平分线上,由线段垂直平分线的性质即可得到结论.
解答  解:(1)把A(0,3),C(3,0)代y2=k2x+b2$\left\{\begin{array}{l}{b=3}\\{3x+b=0}\end{array}\right.$,
解:(1)把A(0,3),C(3,0)代y2=k2x+b2$\left\{\begin{array}{l}{b=3}\\{3x+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$.
故函数y2的函数关系式y2=-x+3,
把A(0,3),B(1,0)代入y1=k1x+b1得$\left\{\begin{array}{l}{b=3}\\{k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-3}\\{b=3}\end{array}\right.$.
故y1的函数关系式为:y1=-3x+3
(2)S△ABC=$\frac{1}{2}$BC•AO=$\frac{1}{2}×$2×3=3;
(3)∵OA=OC=3,
∴AC=3$\sqrt{2}$,
①当AD=AC=3$\sqrt{3}$时,OD=OC=3,
∴D1(-3,0),
②当AC=CD=3$\sqrt{2}$时,OD=CD-OC=3$\sqrt{2}$-3,
∴D2(3-3$\sqrt{2}$,0),
③当AD=PD=3时,D在AC的垂直平分线上,
∴D与O重合,
∴D3(0,0),
④当AD=CD=3$\sqrt{2}$时,
OD=OC+CD=3+3$\sqrt{2}$,
∴D4(3+3$\sqrt{3}$,0).
综上所述:点D在x轴上,且满足三角形ACD是等腰三角形,D点坐标:(-3,0)(3-3$\sqrt{2}$,0)(0,0)(3+3$\sqrt{2}$,0).
点评 本题考查了两直线相交的问题,三角形的面积,求交点坐标代定系数法求解析式,认真审题,弄清题意是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案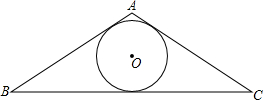 已知:如图,⊙O是△ABC的内切圆,下列说法错误的是( )
已知:如图,⊙O是△ABC的内切圆,下列说法错误的是( )| A. | 点O在△ABC的三边垂直平分线上 | |
| B. | 点O在△ABC的三个内角平分线上 | |
| C. | 如果△ABC的面积为S,三边长为a,b,c,⊙O的半径为r,那么r=$\frac{2S}{a+b+c}$ | |
| D. | 如果△ABC的三边长分别为5,7,8,那么以A、B、C为端点三条切线长分别为5,3,2 |
 已知:△ABC.
已知:△ABC. 如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,求BE的长.
如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,求BE的长. 如图,已知AB=AC,BD=DC,AE平分∠CAF,试判断AE与AD的位置关系,并说明理由.
如图,已知AB=AC,BD=DC,AE平分∠CAF,试判断AE与AD的位置关系,并说明理由.