题目内容
18.如图,在平面直角坐标系中,抛物线W1:y=-x2+6x-5与x轴交于A、B两点,点C是该抛物线的顶点.(1)若抛物线W1与抛物线W2关于直线x=-1对称,其中,点C与点F,点E与点B,点D与点A是对应点,求抛物线W2的表达式.
(2)连接BC,在直线x=-1上找一点H,使得△BCH周长最小,并求出点H的坐标.
(3)连接FD,点P是直线x=-1上一点,点Q是抛物线W1上一点,若以点D、F、P、Q为顶点的四边形是平行四边形,请求出符合条件的点Q的坐标.
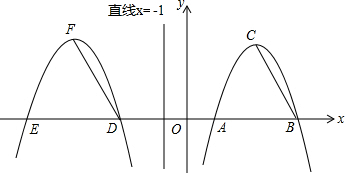
分析 (1)先求得点A、B的坐标,然后利用对称性可得到E、D的坐标,故此W2可看作是W1向左平移8个单位得到;
(2)连结BF交x=-1与H.然后求得直线FB的解析式,在求得当x=-1时,对应的y值,从而可得到点H的坐标;
(3)当DP为平行四边形的对角线时,设点P的坐标为(-1,a),Q(x,y),依据中点坐标公式可知Q(1,a-4),然后将点Q的坐标代入W1的解析式可求得a的值;当DP为平行四边形的边时.设点P的坐标为(-1,a),由PQ∥DF且PQ=DF可知点Q的坐标为(-3,a+4),然后将点Q的坐标代入W1的解析式可求得a的值.
解答 解:(1)令y=0得:0=-x2+6x-5,解得x=1或x=5,
∴A(1,0),B(5,0).
∵点E与段B关于x=-1对称,
∴点E(-7,0).
∴AE=8.
∴W2可由W1向右平移8个单位得到.
∴抛物线W2的表达式为y=-(x+8)2+6(x+8)-5,即y=-x2-10x-21.
(2)如图1所示:连结BF交x=-1与H.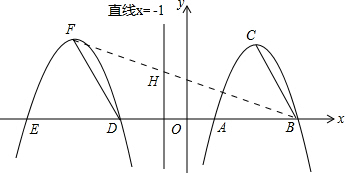
∵y=-x2+6x-5=-(x-3)2+4,
∴C(3,4).
∵点F与点C关于x=-1对称,
∴FH=CH,F(-5,4).
∴当点F、H、B在一条直线上时,HC+BH有最小值,即△BCH的周长最小.
设BF的解析式为y=kx+b,将点B和点F的坐标代入得:$\left\{\begin{array}{l}{-5k+b=4}\\{5k+b=0}\end{array}\right.$,解得:k=-$\frac{2}{5}$,b=2.
∴直线BF的解析式为y=-$\frac{2}{5}$x+2.
当x=-1时,y=$\frac{12}{5}$.
∴H(-1,$\frac{12}{5}$).
(3)当DP为平行四边形的对角线时,设点P的坐标为(-1,a),Q(x,y).
∵平行四边形的对角线互相平分,
∴$\frac{x-5}{2}=\frac{-3-1}{2}$,$\frac{0+a}{2}=\frac{4+y}{2}$,
∴x=1,y=a-4.
∴Q(1,a-4).
将点Q的坐标代入W1的解析式得:a-4=-1+6-5,解得a=4.
∴Q(1,0).
当DP为平行四边形的边时.设点P的坐标为(-1,a).
∵平行四边形的对边平行且相等,
∴PQ可看作由DF平移得到.
∴点Q的坐标为(-1-2,a+4).
将点Q的坐标代入W1的解析式得:a+4=-9+6×(-3)-5,解得a=-36.
∴Q(-3,-32).
综上所述,点Q的坐标为(1,0)或(-3,-32)时,以点D、F、P、Q为顶点的四边形是平行四边形.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了轴对称图形的性质、平移与坐标变化的规律,用含a的式子表示出点Q的坐标是解题的关键.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案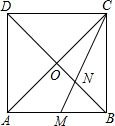 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=4,则线段ON的长为( )
如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=4,则线段ON的长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$ |
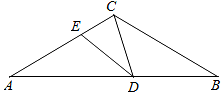 如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.
如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E. 已知线段a,b用尺规作一条线段c,使c=a+b.(不写作法,保留作图痕迹)
已知线段a,b用尺规作一条线段c,使c=a+b.(不写作法,保留作图痕迹)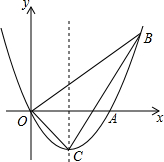 如图,已知抛物线经过点A(2,0),B(3,3)及原点O,顶点为C.
如图,已知抛物线经过点A(2,0),B(3,3)及原点O,顶点为C.